Some useful functions.

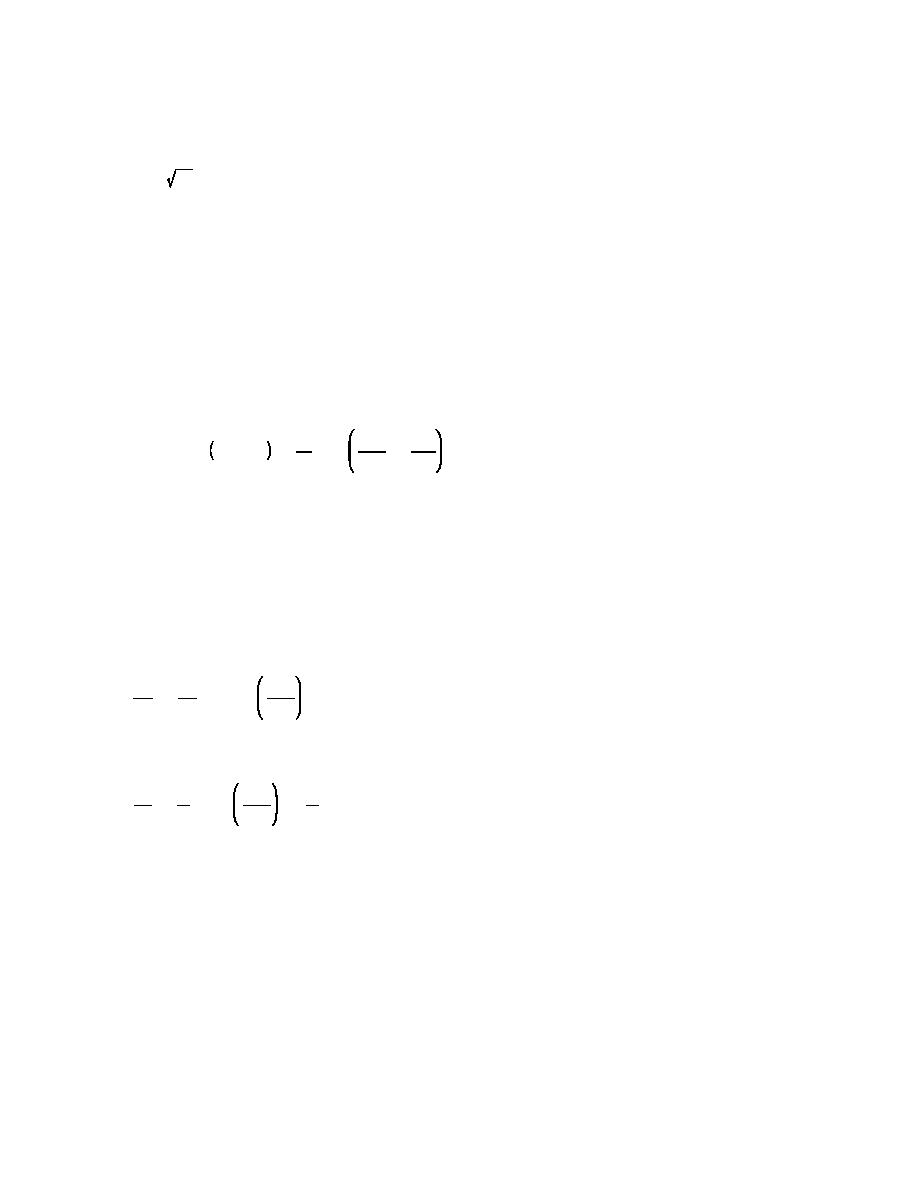
EM 1110-2-1100 (Part II)

30 Apr 02

(n) When the relative water depth becomes shallow, i.e., 2πd/L < 1/4 or d/L < 1/25, Equation II-1-8 can

be simplified to

C ' gd

(II-1-18)

(o) Waves sufficiently long such that Equation II-1-18 may be applied are termed long waves. This

relation is attributed to Lagrange. Thus, when a wave travels in shallow water, wave celerity depends only

on water depth.

(p) In summary, as a wind wave passes from deep water to the beach its speed and length are first only

a function of its period (or frequency); then as the depth becomes shallower relative to its length, the length

and speed are dependent upon both depth and period; and finally the wave reaches a point where its length

and speed are dependent only on depth (and not frequency).

(3) The sinusoidal wave profile. The equation describing the free surface as a function of time t and

horizontal distance x for a simple sinusoidal wave can be shown to be

H

2πx

2πt

cos

' a cos θ

η ' a cos kx & ωt '

(II-1-19)

&

2

L

T

where η is the elevation of the water surface relative to the SWL, and H/2 is one-half the wave height equal

to the wave amplitude a. This expression represents a periodic, sinusoidal, progressive wave traveling in the

positive x-direction. For a wave moving in the negative x-direction, the minus sign before 2πt/T is replaced

with a plus sign. When θ = (2πx/L - 2πt/T) equals 0, π/2, π, 3π/2, the corresponding values of η are H/2, 0,

-H/2, and 0, respectively (Figure II-1-1).

(4) Some useful functions.

(a) Dividing Equation II-1-9 by Equation II-1-13, and Equation II-1-10 by Equation II-1-15 yields,

C

L

2πd

' tanh kd

' tanh

(II-1-20)

'

C0

L0

L

(b) If both sides of Equation II-1-20 are multiplied by d/L, it becomes

d

2πd

d

(II-1-21)

tanh

tanh kd

'

L0

L

(c) The terms d/Lo and d/L and other useful functions such as kd = 2πd/L and tanh (kd) have been

tabulated by Wiegel (1954) as a function of d/Lo (see also SPM 1984, Appendix C, Tables C-1 and C-2).

These functions simplify the solution of wave problems described by the linear theory and are summarized

in Figure II-1-5. An example problem illustrating the use of linear wave theory equations and the figures and

tables mentioned follows.

Water Wave Mechanics

II-1-9