Figure II-1-5. Variation of wave parameters with d/L0 (Dean and Dalrymple 1991)

Part-II-Chap1
Page Navigation
23

EM 1110-2-1100 (Part II)

30 Apr 02

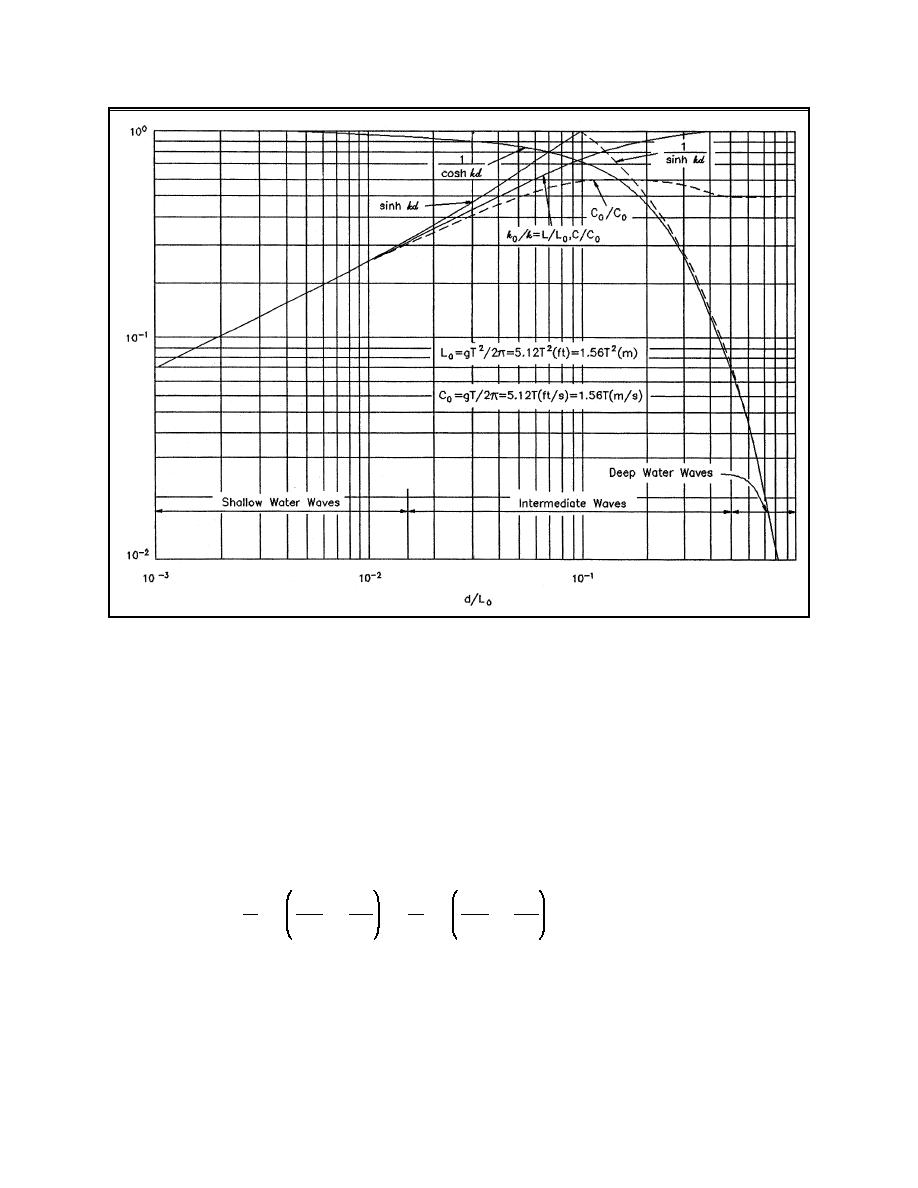
Figure II-1-5. Variation of wave parameters with d/L0 (Dean and Dalrymple 1991)

waves or a wave train travels is generally not identical to the speed with which individual waves within the

group travel. The group speed is termed the group velocity Cg; the individual wave speed is the phase velocity

or wave celerity given by Equations II-1-8 or II-1-9. For waves propagating in deep or transitional water with

gravity as the primary restoring force, the group velocity will be less than the phase velocity. For those

waves, propagated primarily under the influence of surface tension (i.e., capillary waves), the group velocity

may exceed the velocity of an individual wave.

(b) The concept of group velocity can be described by considering the interaction of two sinusoidal wave

trains moving in the same direction with slightly different wavelengths and periods. The equation of the

water surface is given by

2πx

2πt

2πx

2πt

η ' η1 % η2 '

cos

(II-1-47)

where η1 and η2 are the two components. They may be summed since superposition of solutions is

permissible when the linear wave theory is used. For simplicity, the heights of both wave components have

been assumed equal. Since the wavelengths of the two component waves, L1 and L2, have been assumed

slightly different for some values of x at a given time, the two components will be in phase and the wave

height observed will be 2H; for some other values of x, the two waves will be completely out of phase and

Water Wave Mechanics

II-1-23