Cnoidal wave theory.

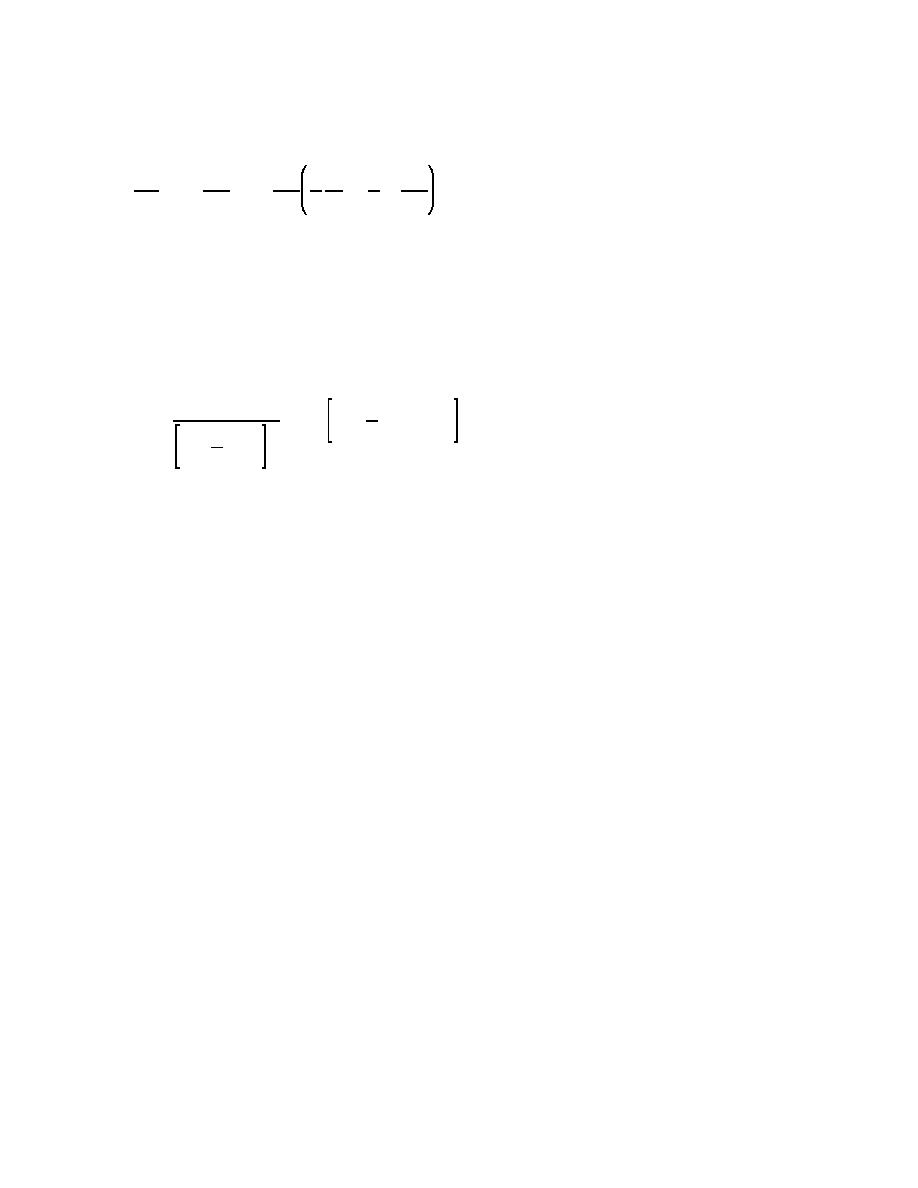
EM 1110-2-1100 (Part II)

30 Apr 02

which are termed the Boussinesq equations (Whitham 1967; Peregrine 1972; Mei 1991). Originally,

Boussinesq used the horizontal velocity at the bottom. Eliminating yields (Miles 1979, 1980, 1981)

M2η

M2 3 η2

1 2 M2η

% d

& gd

' gd

(II-1-74)

2 2 d

3 Mx 2

2

Mt

Mx

A periodic solution to Equation II-1-74 is of the form

η ' a e i(kx & ωt) ' a cos θ

(II-1-75)

u ' U0 e i(kx & ωt) ' U0 cos θ

which has a dispersion relation and an approximation to it given by

Cs

1

(k d) 2 % ...

. Cs 1 &

C'

(II-1-76)

3

1/2

1

(k d) 2

1%

3

The term 1/3 (kd)2 in Equation II-1-76 represents the dispersion of wave motion.

(c) The most elementary solution of the Boussinesq equation is the solitary wave (Russell 1844; Fenton

1972; Miles 1980). A solitary wave is a wave with only crest and a surface profile lying entirely above the

SWL. Fenton's solution gives the maximum solitary wave height, Hmax = 0.85 d and maximum propagation

speed C2max = 1.7 gd. Earlier research studies using the solitary waves obtained Hmax = 0.78 d and C2max =

1.56 gd. The maximum solitary-amplitude wave is frequently used to calculate the height of breaking waves

in shallow water. However, subsequent research has shown that the highest solitary wave is not necessarily

the most energetic (Longuet-Higgins and Fenton 1974).

(4) Cnoidal wave theory.

(a) Korteweg and de Vries (1895) developed a wave theory termed the cnoidal theory. The cnoidal

theory is applicable to finite-amplitude shallow-water waves and includes both nonlinearity and dispersion

effects. Cnoidal theory is based on the Boussinesq, but is restricted to waves progressing in only one

direction. The theory is defined in terms of the Jacobian elliptic function, cn, hence the name cnoidal.

Cnoidal waves are periodic with sharp crests separated by wide flat troughs (Figure II-1-10).

(b) The approximate range of validity of the cnoidal theory is d/L < 1/8 when the Ursell number UR >

20. As wavelength becomes long and approaches infinity, cnoidal wave theory reduces to the solitary wave

theory, which is described in the next section. Also, as the ratio of wave height to water depth becomes small

(infinitesimal wave height), the wave profile approaches the sinusoidal profile predicted by the linear theory.

(c) Cnoidal waves have been studied extensively by many investigators (Keulegan and Patterson 1940;

Keller 1948; Laitone 1962) who developed first- through third-order approximations to the cnoidal wave

theory. Wiegel (1960) summarized the principal results in a more usable form by presenting such wave

characteristics as length, celerity, and period in tabular and graphical form to facilitate application of cnoidal

theory.

(d) Wiegel (1964) further simplified the earlier works for engineering applications. Recent additional

improvements to the theory have been made (Miles 1981; Fenton 1972, 1979). Using a Rayleigh-Boussinesq

Water Wave Mechanics

II-1-37