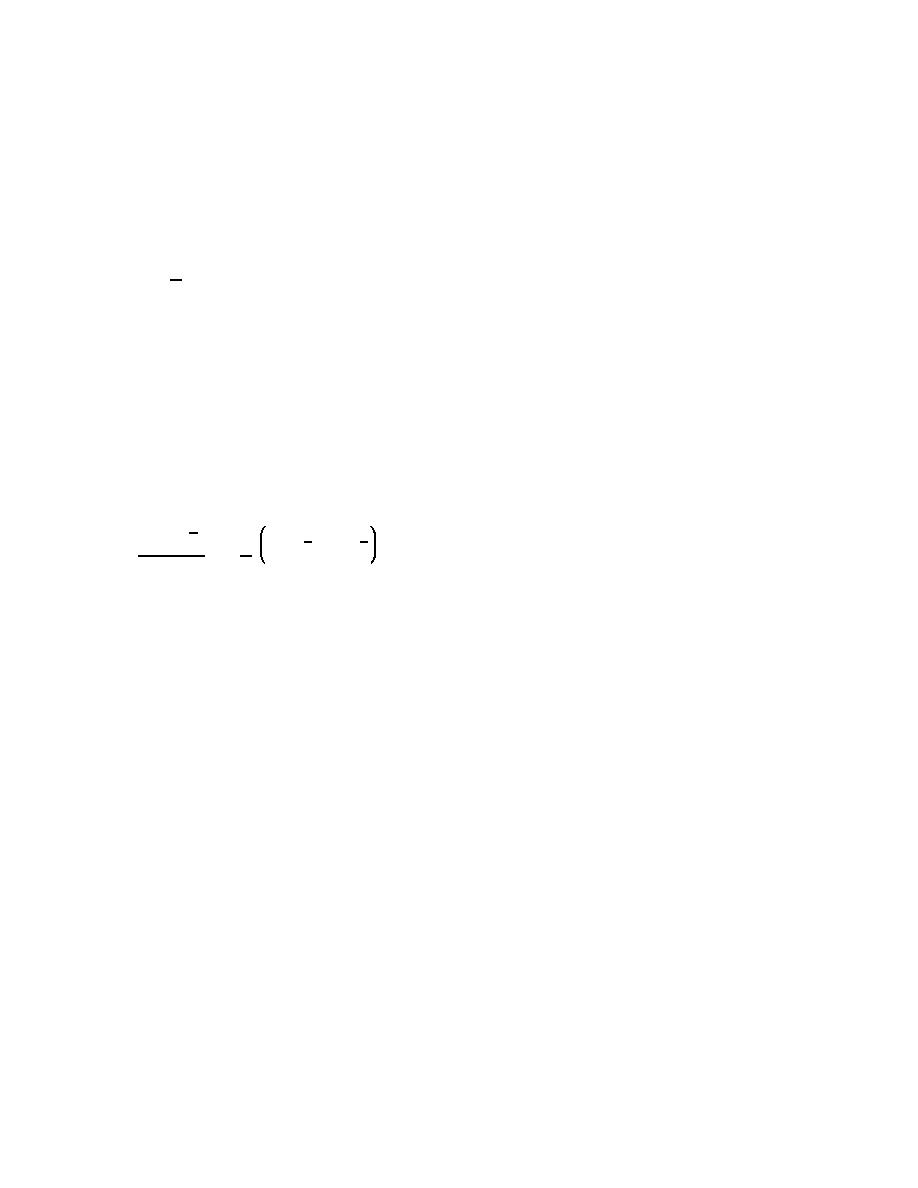
EM 1110-2-1100 (Part II)
31 July 2003
where E is the wave energy per unit surface area, Cg is the wave group speed, and δ is the energy dissipation
rate per unit surface area due to wave breaking. The wave energy flux ECg may be specified from linear or
higher order wave theory. Le Mhaut (1962) approximated a breaking wave as a hydraulic jump and
substituted the dissipation of a hydraulic jump for δ in Equation II-4-13 (see also Divoky, Le Mhaut, and
Lin 1970; Hwang and Divoky 1970; Svendsen, Madsen, and Hansen 1978).
(b) Dally, Dean, and Dalrymple (1985) modeled the dissipation rate as
κ
(E Cg & E Cg , s )
δ'
(II-4-14)
d
where κ is an empirical decay coefficient, found to have the value 0.15, and ECg,s is the energy flux associated
with a stable wave height
Hstable ' Γ d
(II-4-15)
(c) The quantity Γ is an empirical coefficient with a value of approximately 0.4. The stable wave height
is the height at which a wave stops breaking and re-forms. As indicated, this approach is based on the
assumption that energy dissipation is proportional to the difference between local energy flux and stable
energy flux. Applying linear, shallow-water theory, the Dally, Dean, and Dalrymple model reduces to
1
1
5
d (H 2 d )
2
κ
H 2d & Γ 2d
2
2
for
H > Hstable
'&
(II-4-16)
dx
d
'0
for
H < Hstable
This approach has been successful in modeling wave transformation over irregular beach profiles, including
bars (e.g., Ebersole (1987), Larson and Kraus (1991), Dally (1992)).
(3) Irregular waves.
(a) Transformation of irregular waves through the surf zone may be analyzed or modeled with either a
statistical (individual wave or wave height distribution) or a spectral (parametric spectral shape) approach.
Part II-1 gives background on wave statistics, wave height distributions, and parametric spectral shapes.
(b) The most straightforward statistical approach is transformation of individual waves through the surf
zone. Individual waves seaward of breaking may be measured directly, randomly chosen from a Rayleigh
distribution, or chosen to represent wave height classes in the Rayleigh distribution. Then the individual
waves are independently transformed through the surf zone using Equation II-4-13. Wave height distribution
can be calculated at any point across the surf zone by recombining individual wave heights into a distribution
to calculate wave height statistics (e.g., H1/10 , H1/3 , Hrms). This method does not make a priori assumptions
about wave height distribution in the surf zone. The individual wave method has been applied and verified
with field measurements by Dally (1990), Larson and Kraus (1991), and Dally (1992). Figure II-4-4 shows
the nearshore transformation of Hrms with depth based on the individual wave approach and the Dally, Dean,
and Dalrymple (1985) model for deepwater wave steepness (Hrmso / Lo) of 0.005 to 0.05 and plane beach
slopes of 1/100 and 1/30.
(c) A numerical model called NMLONG (Numerical Model of the LONGshore current) (Larson and
Kraus 1991) calculates wave breaking and decay by the individual wave approach applying the Dally, Dean,
II-4-8
Surf Zone Hydrodynamics




 Previous Page
Previous Page
