EM 1110-2-1100 (Part II)
30 Apr 02
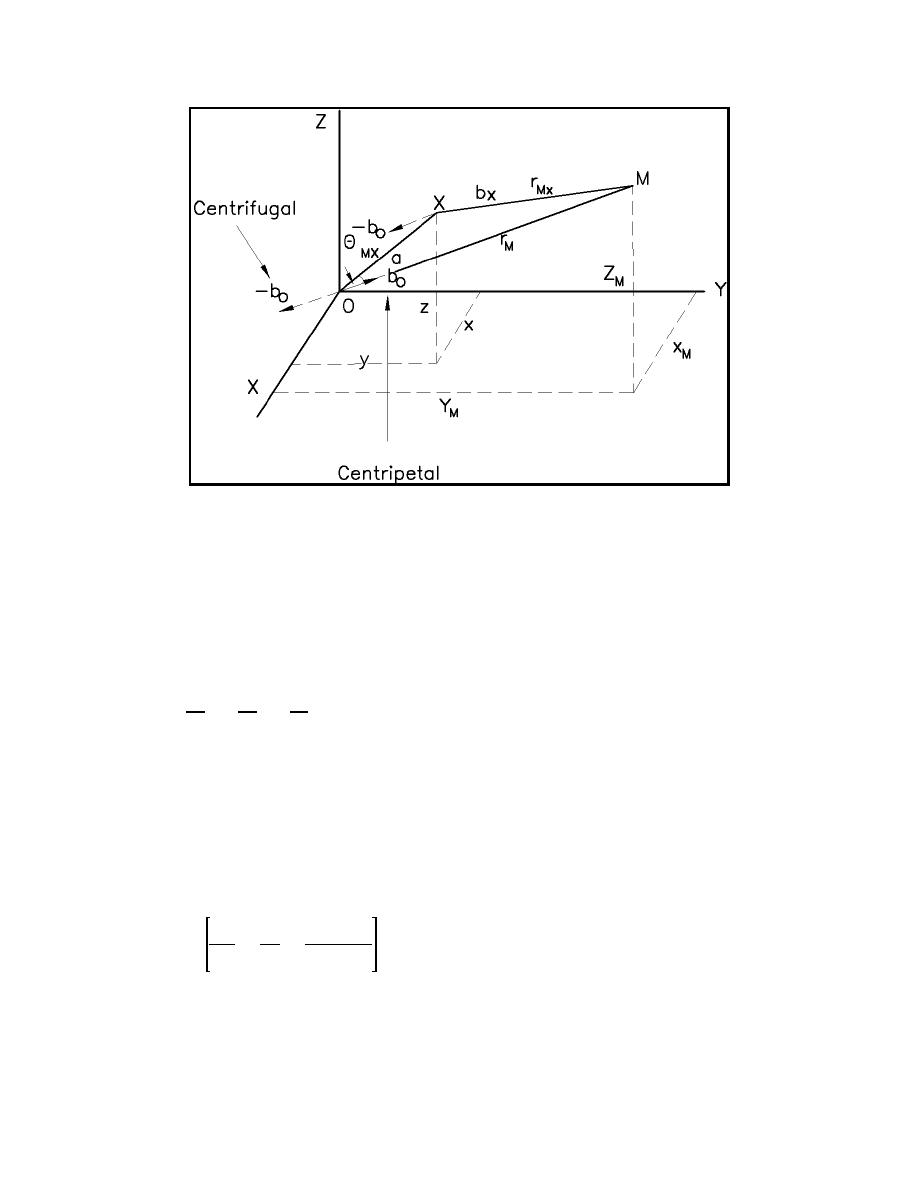
Figure II-5-4.
Schematic diagram of tidal potential (Dronkers 1964)
where the separation distance rMX = [(xm - x)2 + (ym - y)2 + (zm - z)2]1/2 with an equivalent expression for rSX.
(d) The attractive force of the moon and sun at any point X is defined as
P
bX ' L [VM (X) % VS (X)]
(II-5-10)
where L is the vector gradient operator defined as
P
%M
%M
L ' (M
)
(II-5-11)
Mx
My
Mz
(e) From Figure II-5-4, the attractive force at the center of the earth (centripetal) bO is balanced by the
centrifugal force -bO (i.e., equal in magnitude but opposite in direction). Because any point on the earth
experiences the same centrifugal force as that at O, the resultant force at any point X will be equal to bX - bO.
This resultant force difference is the tide generating force, the force that causes the oceans to deform in order
to balance the sum of external forces. Therefore, the difference between the tidal potential at point O and at
point X becomes the tidal potential responsible for the tide-producing forces.
(f) The moon's tide-generating potential can be written as
a cos θMX
1
1
VM ' f M
(II-5-12)
&
&
rMX
rM
rM2
with the tide potential for the sun written as
Water Levels and Long Waves
II-5-7




 Previous Page
Previous Page
