EM 1110-2-1100 (Part II)
30 Apr 02
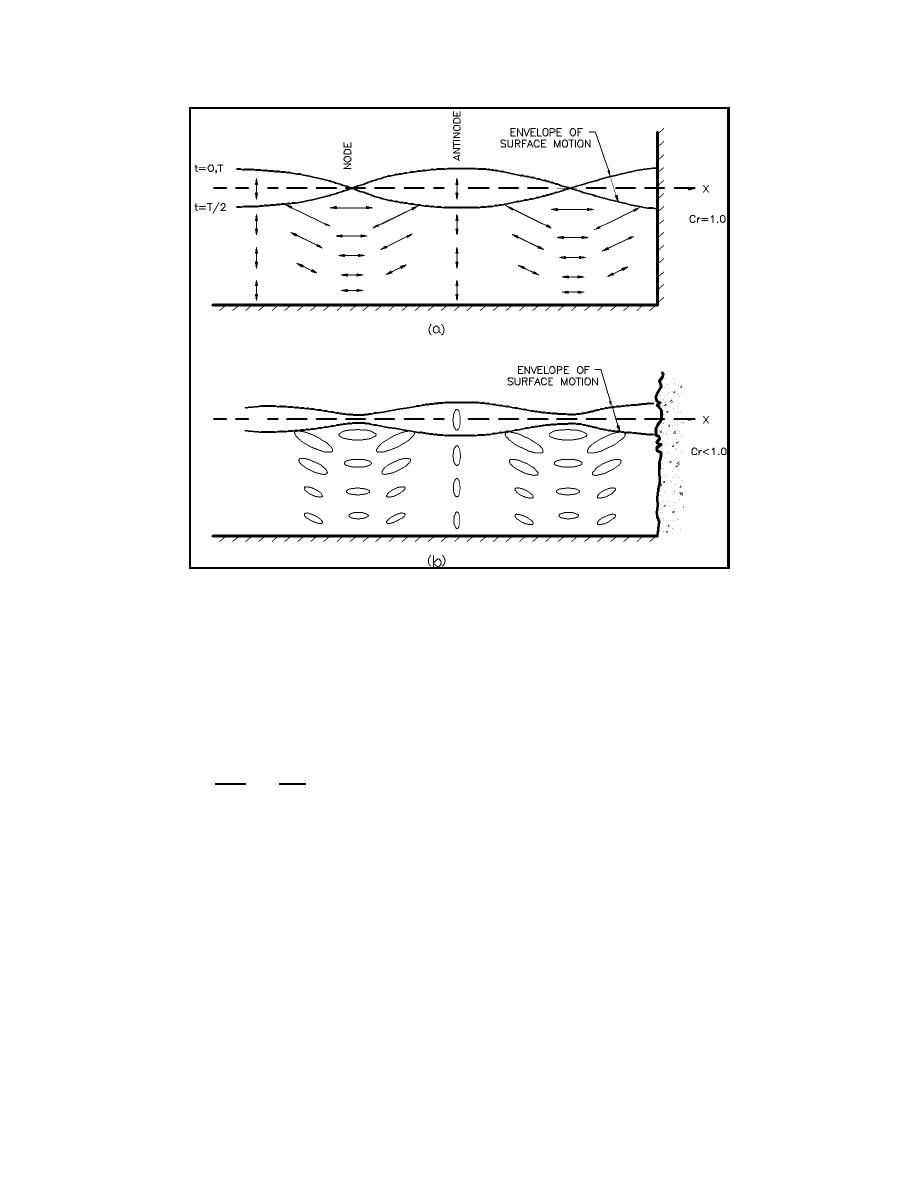
Figure II-7-23. Complete and partial reflection
where α is the angle the slope forms with the horizontal and L0 is the length of the incident wave in deep
water.
(4) Figure II-7-23a is a profile view of the water surface envelope positions for a wave reflecting from
a wall that has a reflection coefficient equal to unity (i.e., Hi = Hr). The water surface amplitude is given by
2πx
2 πt
N ' Hi cos
(II-7-7)
cos
L
T
where L and T are the incident and reflected wave length and period respectively, x is the horizontal ordinate
and t is the time elapsed. The figure also shows the water particle paths at key points. At nodal points, water
particle motions are horizontal and at antinodes, water particle motions are vertical. At t = 0, T/2, and T, the
water is instantaneously still and all of the wave energy is potential energy. At t = T/4 and 3T/4, the water
surface is horizontal and all of the energy is kinetic energy.
(5) When the wall reflection coefficient is less than unity, the water surface envelope positions and
particle paths are as depicted in Figure II-7-23b. As the reflection coefficient decreases toward zero, the
water surface profile and water particle path changes toward the form of a normal progressive wave.
Harbor Hydrodynamics
II-7-27




 Previous Page
Previous Page
