EM 1110-2-1100 (Part II)
30 Apr 02
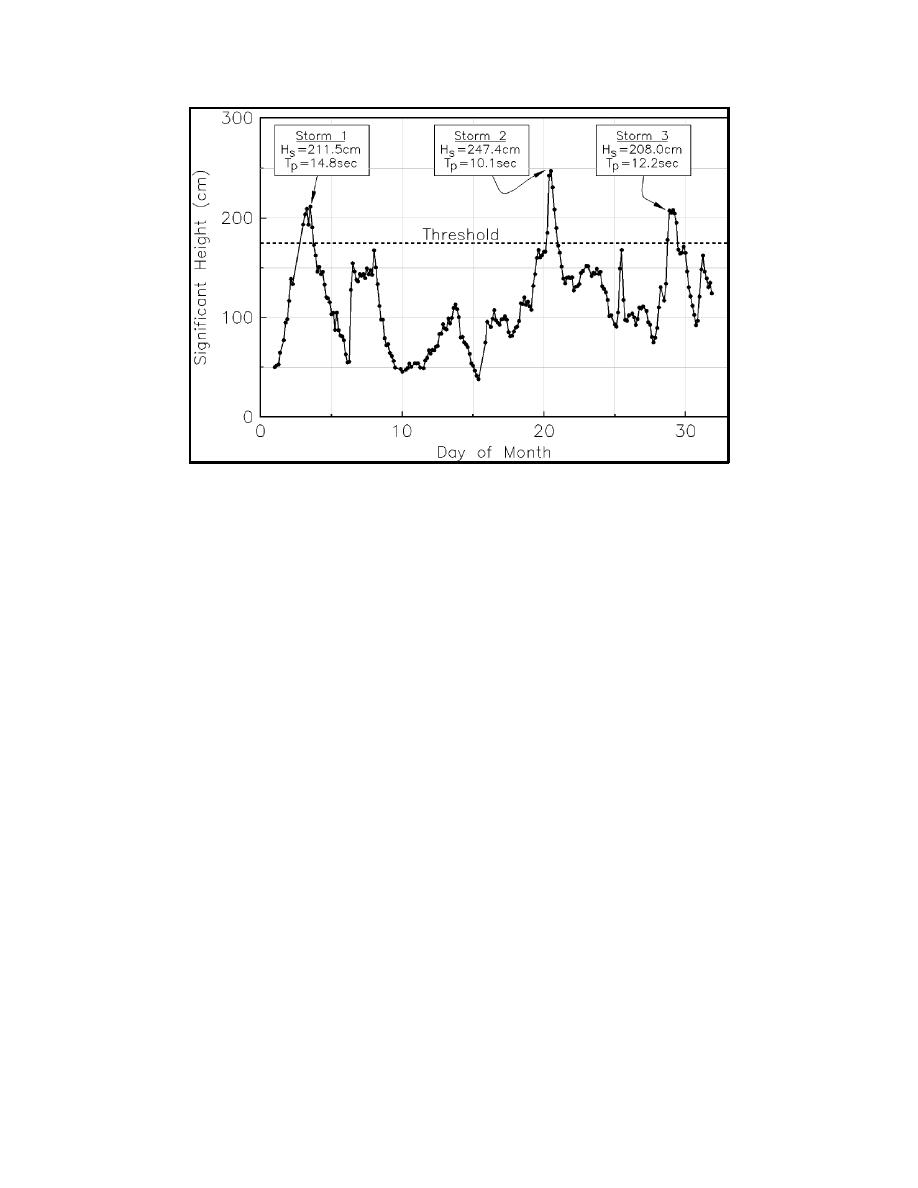
Figure II-8-4.
Selection of extreme values for a partial duration series
Part II-8-5-c. There is no strong theoretical reason for preferring one distribution function over another. The
single sample cannot be expected to fit the true distribution function exactly, especially for the few largest
events. For some processes, such as water levels, one particular distribution function is generally accepted
for all applications. For other processes, such as significant wave heights, a best-fitting distribution function
is often chosen from among several candidates.
(b) Typically, extreme data values are sorted into descending order. A nonexceedance probability must
be assigned to each extreme data value. These plotting positions should be chosen so that the distribution
function can be accurately estimated. Figure II-8-5 gives the commonly used traditional plotting position
formula. The figure also gives formulas developed to remove bias and minimize rms errors when fitting to
specific distribution functions (Goda 1988, Goda and Kobune 1990).
(3) Approaches to estimating parameters. The following approaches can be used to determine parameters
for each candidate distribution function:
(a) Graphical approach. Traditionally, the goodness of fit was determined visually by plotting the data
along with candidate distribution functions. By scaling the plotting axes to make a candidate distribution
appear as a straight line, the parameters of a visually optimum distribution function can more easily be
determined.
(b) Computational approach. An automated computational approach is more objective (though not
necessarily more accurate) and often easier to apply than the relatively tedious graphical approach. Three
alternatives are the least squares method, the maximum likelihood method, and the method of moments. The
least squares method is simplest and, with two-parameter distribution functions, it is often used. It is included
in the ACES software package. One caution with this approach is that it is sensitive to even one or two
extreme points that deviate greatly from the general trend of the data (outliers). The maximum likelihood
method has the advantage of being less likely to produce erratic results when the data contain outliers or differ
somewhat from the distribution function (Mathiesen et al. 1994). More information on computational
approaches is also available from Goda (1988, 1990). Regardless of the method used, it is
II-8-10
Hydrodynamic Analysis and Design Conditions




 Previous Page
Previous Page
