EM 1110-2-1100 (Part V)
31 Jul 2003
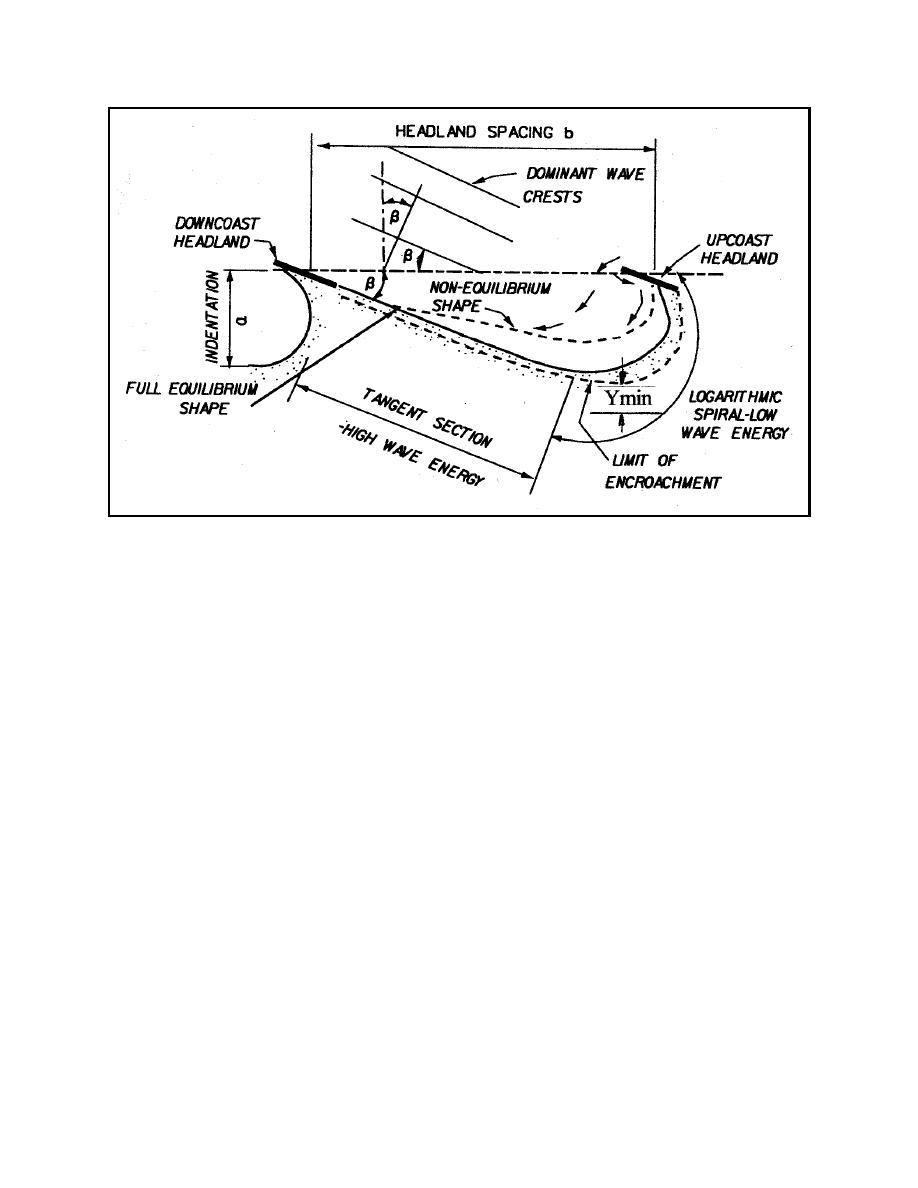
Figure V-3-12. Definition sketch of artificial headland system and beach planform (from EM 1110-2-1617)
(a) Parabolic bay shape. A new empirical approach that uses shoreline data from bays in static
equilibrium and physical models has been developed by Hsu, Silvester, and Xia (1987, 1989). It is called a
parabolic model because the data has been used to fit a second order polynomial. Figure V-3-13 presents a
definition sketch of the four key geometric variables, R, Ro, β and θ, that form the parabolic model. The
model center now exactly matches the initial diffraction point. Part III-2-3-i presents complete details
including definitions of R, Ro, β and θ; the parabolic model equation (2-24); the three coefficients Co,C1, C2
related to wave angle β in Figure III-2-27 and limitations of the data. An Example Problem III-2-8 is also
presented to illustrate an application of the model which assumes one predominant wave direction exists at
the site of interest. Many more examples and discussion is found in Silverster and Hsu 1993.
(b) Minimum width for storm protection. As illustrated in Figure V-3-12, storm waves may be from a
different direction to cut back the beach and form a new limit of encroachment planform shape. A more
detailed definition sketch in perspective and cross section is presented in Figure V-3-14 (adopted from
Hardaway, Thomas, and Li 1991). Two nearshore breakwaters together with beach nourishment form the
headland breakwater design for shore protection. The following terms are defined:
Length of breakwater structure
Ls
Lg
Gap distance between adjacent breakwaters
ds
Depth (average) at breakwater below mean water level
e
Erosion of shoreline (mhw) from design storm
Yo
Distance of breakwater from original shoreline
Yg
Maximum indentation under normal wave conditions
Shore Protection Projects
V-3-39




 Previous Page
Previous Page
