EM 1110-2-1100 (Part V)
31 Jul 2003
EXAMPLE PROBLEM V-4-8
FIND:
The "half-life" of the specified beach fills (time at which 50 percent of the beach-fill material
remains within the placement area).
GIVEN:
Both projects have a rectangular planform with an alongshore length of 6 km. The effective
breaking wave height at beach fill A is 0.80 m whereas the effective breaking wave height at beach
fill B is 0.95 m.
Cgb = (g hb)1/2
ρs/ρ = 2.65
n = 0.4
K = 0.77
g = 9.81 m/s2
hb = Hb/0.78
db = 2.5 m
dc = 6.0 m
SOLUTION:
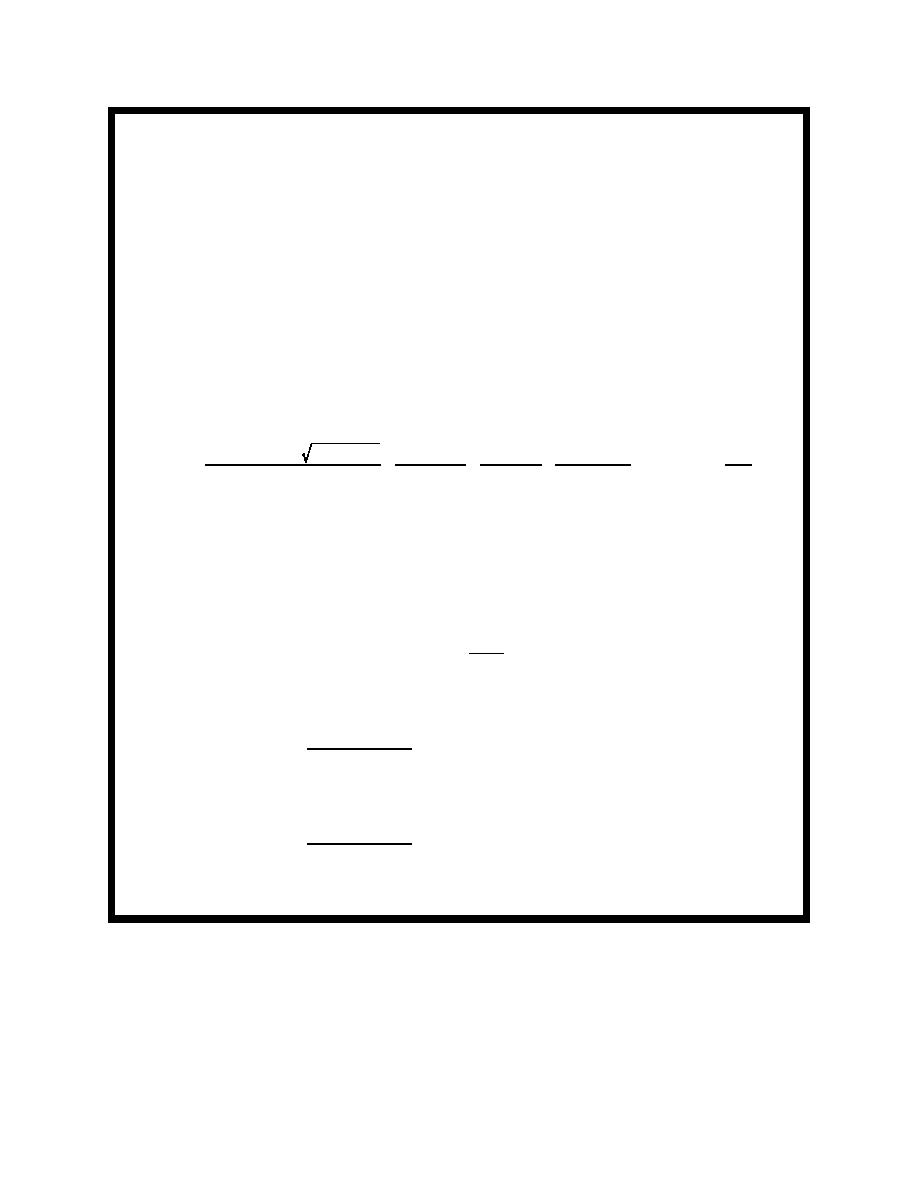
Equation III-2-26 gives: (for beach fill A)
0.77 (0.80)2.5 9.81/0.78
m2
1
1
1
ε'
.
.
.
' 0.02322
8
(2.65 & 1) (1 & 0.4) (2.5 % 6.0)
sec
(for beach fill B)
ε = 0.03568 m2/sec (see EXAMPLE PROBLEM V-4-7)
Solving Equation V-4-12 for t and p(t) = 0.5 gives
a2 π
t50%
'
4ε
Half-life of beach fill A
(3000)2 (3.14)
' 304.420 X 106 sec 9.65 years
t50%
'
(4) (0.02322)
Half-life of beach fill B
(3000)2 (3.14)
' 198.102 X 106 sec 6.28 years
t50%
'
(4) (0.03568)
where ∆ yo is the initial dry beach width (after cross-shore equilibration), E is the historical shoreline
recession rate and a is the beach-fill half length. Example Problem V-4-9 illustrates the effect of background
erosion rate. Comparison of results from this example with results from Example V-4-7 show that the
specified background erosion rate decreased the half-life of the fill by about 20 percent. Note that the
historical shoreline erosion rate E, may underestimate the postnourishment erosion rate if the preproject beach
is armored or otherwise features a deficit in sand volume or sand supply.
Beach Fill Design
V-4-53




 Previous Page
Previous Page
