EM 1110-2-1100 (Part III)
30 Apr 02
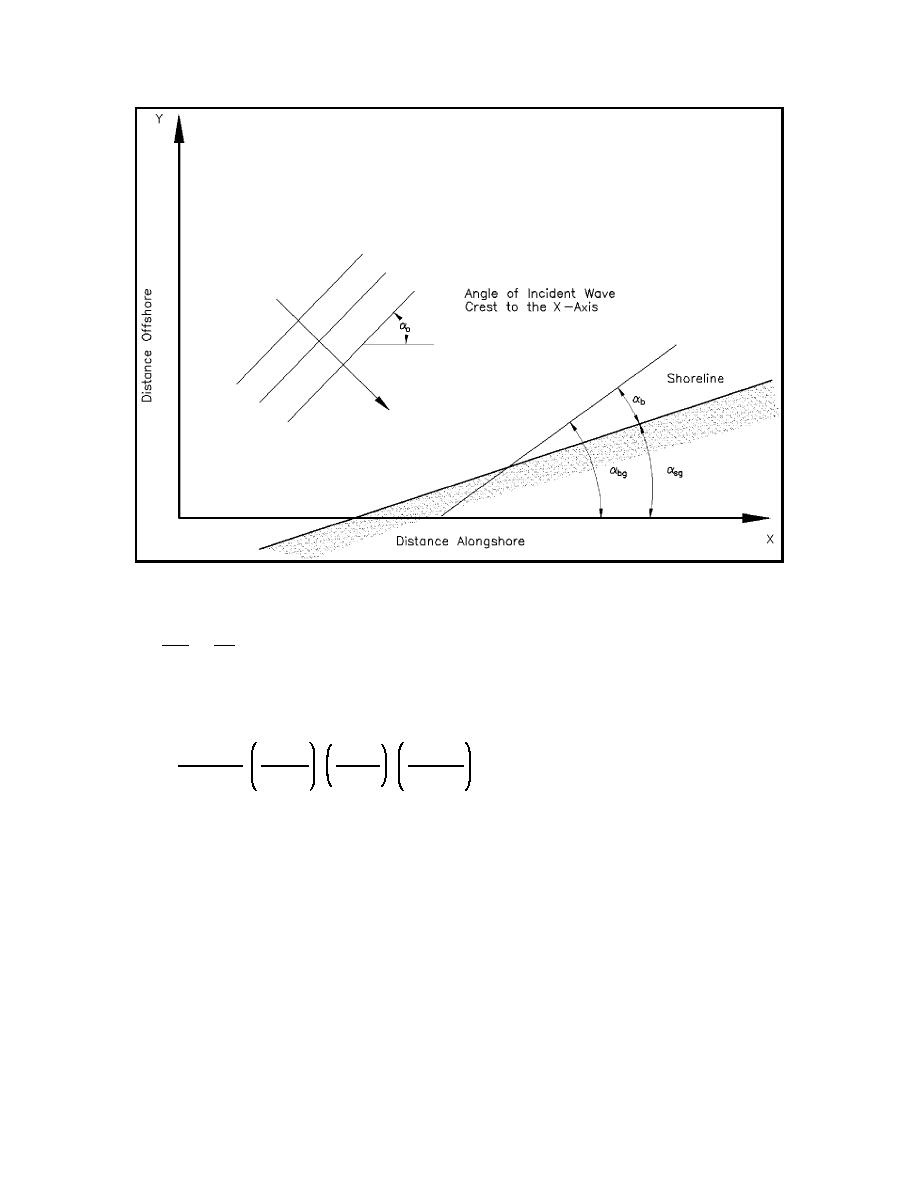
Figure III-2-29.
Definition of local breaker angle
M2 y
My
ε
'
(III-2-25)
Mt
Mx 2
where
2
K Hb Cg b
ρ
1
1
ε'
(III-2-26)
8
ρs & ρ
dB % dc
1&n
and where dB = beach berm height above still-water level; dc = depth of appreciable sand transport as
measured from still-water level. Equation 2-25 is a partial differential equation, as it is dependent on both
space (variable x) and time (variable t). A number of researchers have employed this equation or slight varia-
tions of it to provide analytical solutions to shoreline change under certain assumptions (the boundary con-
ditions and initial conditions of the problem). Pelnard-Considre (1956) first presented an analytical solution
to this simplified shoreline change equation for the case of an impermeable groin or jetty impounding the
longshore sand transport on the updrift side of the structure under a stationary (constant) wave climate.
Pelnard-Considre also verified its applicability with laboratory experiments and derived analytical solutions
of the linearized shoreline change equation for two other boundary conditions: shoreline evolution updrift
of an impermeable groin (with bypassing) and release of an instantaneous plane source of sand on the beach.
Longshore Sediment Transport
III-2-57




 Previous Page
Previous Page
