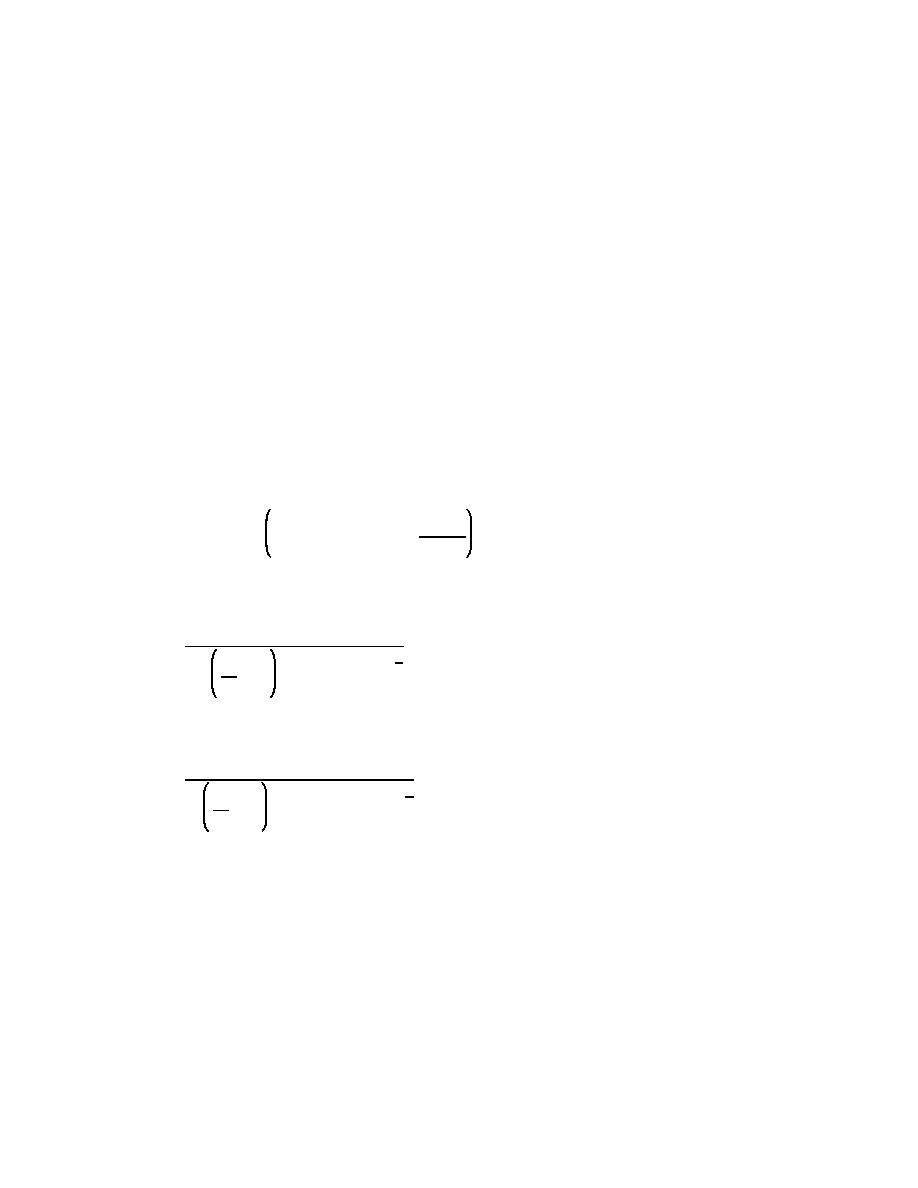
EM 1110-2-1100 (Part III)
30 Apr 02
more complex conditions, such as time-varying wave conditions, large shoreline angles, variable longshore
wave height (perhaps due to diffraction), multiple structures, etc., numerical models can be used in many
instances.
b.
Shoreline Change Model GENESIS.
(1) Overview.
(a) The numerical model GENESIS (Hanson 1987; Hanson and Kraus 1989; Gravens, Kraus, and
Hanson 1991) is an example of a one-line shoreline change model that is supported for use both on personal
computer and mainframe systems (see Cialone et al. (1992)) and has a companion system of support programs
(Gravens 1992). GENESIS has been applied to numerous coastal engineering projects, and it calculates
shoreline change due to spatial and temporal differences in longshore transport as produced by breaking
waves. GENESIS is used in conjunction with grid-based wave transformation models that develop values
of breaking wave height and angle for various representative wave periods and approach azimuths along the
coast. Shoreline change at grid cells along the coastline is computed in the time domain as a function of these
computed values of the breaking wave height and angle.
(b) As discussed by Hanson (1987) and Hanson and Kraus (1989), the empirical predictive formula for
the longshore sand transport rate used in GENESIS is
dHb sig
H 2b sig
(III-2-42)
QR '
Cgb a1 sin2αb & a2 cosαb
dx
The nondimensional parameters a1 and a2 are given by
K1
a1 '
5
(III-2-43)
ρs
2
&1
(1 & n) (1.416)
16
ρ
and
K2
a2 '
7
(III-2-44)
ρs
2
&1
(1 & n) m (1.416)
8
ρ
where K1 and K2 are empirical coefficients, treated as calibration parameters, and m is the average bottom
slope from the shoreline to the depth of active longshore sand transport. The factors involving 1.416 are used
to convert the K1 and K2 coefficients from use with rms wave height to use with significant wave height
(which is the statistical wave height required by GENESIS). That is, Equation 2-43 is presented such that
K1 is equivalent to Krms (as opposed to Ksig) in Equation 2-7. Nonetheless, both longshore sand transport
coefficients K1 and K2 should be viewed as calibration parameters that are to be adjusted to match measured
positions of shoreline change (Hanson and Kraus 1989).
(c) The first term in Equation 2-42 corresponds to Equation 2-7, and accounts for longshore sand
transport produced by obliquely incident breaking waves. The second term in Equation 2-42 is used to
describe the effect of another generating mechanism for longshore sand transport, the longshore gradient in
breaking wave height. The contribution arising from the longshore gradient in wave height is usually much
III-2-80
Longshore Sediment Transport




 Previous Page
Previous Page
