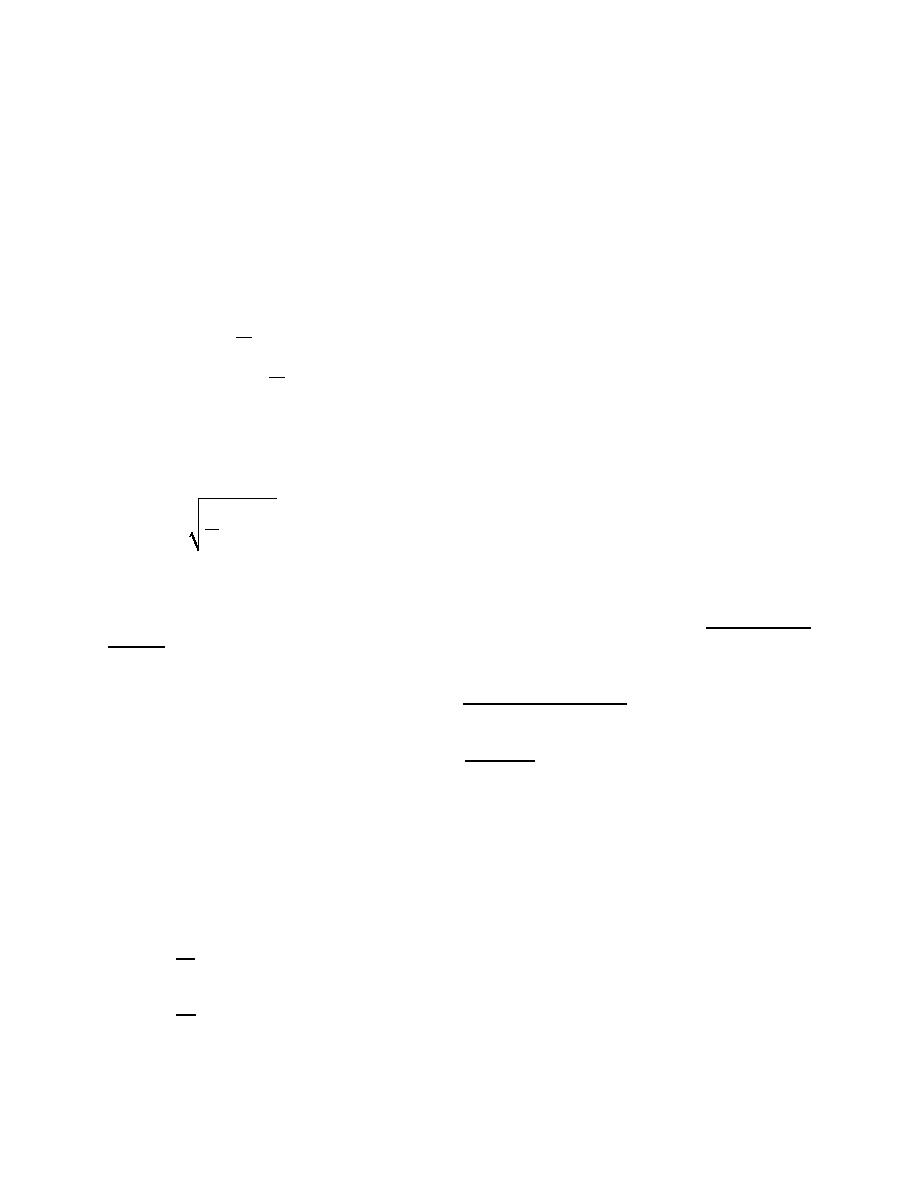
EM 1110-2-1100 (Part II)
30 Apr 02
all the measured wave heights is the rms wave height Hrms. The average height of the largest 1/n of all waves
in the record is the H1/n where n = 10, 11, 12, 13,..., 99, 100 are common values. For instance, H1/10 is the
mean height of the highest one-tenth waves. In coastal projects, engineers are faced with designing for the
maximum expected, the highest possible waves, or some other equivalent wave height. From one wave record
measured at a point, these heights may be estimated by ordering waves from the largest to the smallest and
assigning to them a number from 1 to N. The significant wave height H1/3 or Hs will be the average of the first
(highest) N/3 waves.
(e) The probability that a wave height is greater (less) than or equal to a design wave height Hd may be
found from
m
P(H > Hd) '
N
(II-1-114)
m
P(H # Hd) ' 1 &
N
where m is the number of waves higher than Hd. For an individual observed wave record the probability
distribution P(H > Hd) can be formulated in tabular form and possibly fitted by some well-known distribution.
The root-mean-square wave height Hrms may be computed as
j Hj
N
1
2
Hrms '
(II-1-115)
N j'1
in which Hj denote the ordered individual wave heights in the record.
(f) Probability distributions discussed in the irregular wave section of the CEM refer to short term wave
statistics. This subject concerns the probability that a wave of a given height will occur given that we know
the statistics of the sea surface over a 16- to 60-min period. A short-term wave statistics question might be,
for example, "If we have measured the waves for 15 min and found that Hs is 2m, what is the chance that a
wave of 4 m may occur?" This must be contrasted to long-term wave statistics. To obtain long-term wave
statistics, a 15-min record may have been recorded (and statistics of each record computed) every 3 hr for 10
years (about 29,000 records) and the statistics of the set of 29,000 significant wave heights compiled. A long-
term wave statistics question might be, "If the mean significant wave height may be 2m with a standard
deviation of 0.75m, what is the chance that once in 10 years the significant wave height will exceed 4 m?"
These are two entirely different statistical questions and must be treated differently.
(g) A similar approach can be used for the wave period. The mean zero-crossing period is called the
zero-crossing period Tz. The average wave period between two neighboring wave crests is the wave crest
period Tc. Therefore, in the time domain wave record analysis, the average wave period may also be obtained
from the total length of record length Tr either using Tz or Tc (Tucker 1963). These periods are related to Tr
by
Tr
Tz '
Nz
(II-1-116)
Tr
Tc '
Nc
Water Wave Mechanics
II-1-67



 Previous Page
Previous Page
