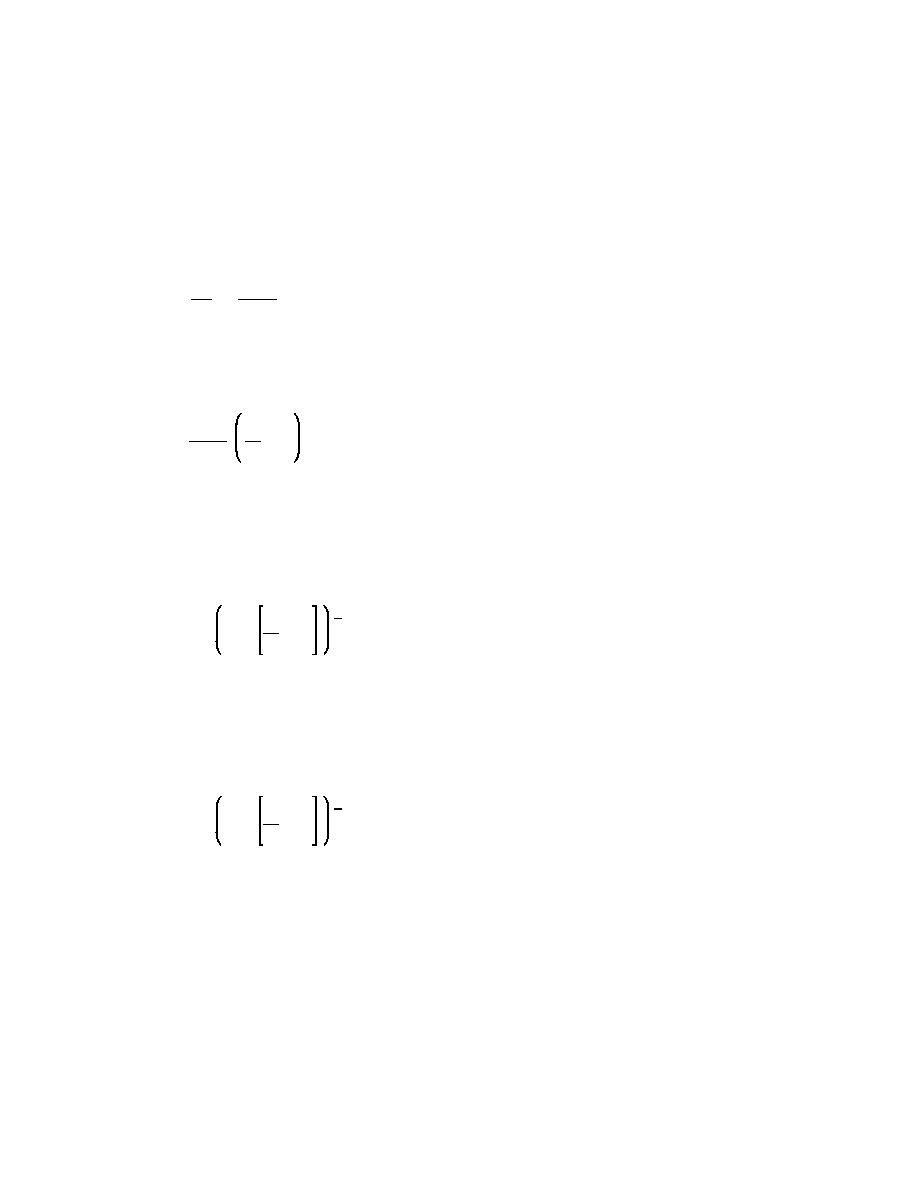
EM 1110-2-1100 (Part III)
30 Apr 02
Re > 400 to Re < 200,000. Here the drag coefficient has the approximately constant value of 0.4 to 0.6. In
this range the particles are larger and denser, and the fall velocity is faster. The physical reason for this
change in the behavior of CD is that inertial drag forces have become predominant over the viscous forces,
and the wake behind the particle has become turbulent. At about Re = 200,000 the drag coefficient decreases
abruptly. This is the region of very large particles at high fall velocities. Here, not only is the wake turbulent,
but the flow in the boundary layer around the particle is turbulent as well.
(4) In the first region, Stokes found the analytical solution for CD as:
24
24 ν
'
'
CD
(III-1-8)
Wf D
Re
(5) This line is labeled "Stokes" in Figure III-1-5. Substituting Equation 1-8 into Equation 1-7 gives the
fall velocity in this region:
ρs
g D2
(III-1-9)
Wf '
&1
18 ν
ρ
(6) Note that in this region the velocity increases as the square of the grain diameter, and is dependent
upon the kinematic viscosity.
(7) For the region of 400 < Re < 200,000, the approximation CD~0.5 is used in Equation 1-7 to obtain:
1
ρs
2
(III-1-10)
&1
Wf ' 1.6 g D
ρ
(8) Here it is seen that the fall velocity varies as the square root of the grain diameter and is independent
of the kinematic viscosity.
(9) Similarly, in the region Re > 200,000, the approximation CD~0.2 is used in Equation 1-7 to obtain:
1
ρs
2
(III-1-11)
&1
' 2.6 g D
Wf
ρ
(10) There is a large transition region between the first two regimes (between 0.5 < Re < 400). For
quartz spheres falling in water, these Reynolds numbers correspond to grain sizes between about 0.08 mm
and 1.9 mm. Unfortunately, this closely corresponds to all sand particles, as seen in Table III-1-2. Thus, for
very small particles (silts and clays), the fall velocity is proportional to D2 and can be calculated from
Equation 1-9. For gravel size particles the fall velocity is proportional to D and can be calculated from
Equation 1-10. However, for sand, the size of most interest to coastal engineers, no simple formula is
available. The fall velocity is in a transition region between a D2 dependence and a D dependence. In this
size range, it is easiest to obtain a fall velocity value from plots such as Figure III-1-6, which show the fall
velocity as a function of grain diameter and water temperature for quartz spheres falling in both water and
air. The vertical and horizontal axes are grain diameter and fall velocity, in millimeters and centimeters per
second, respectively. The short straight lines crossing the curves obliquely are various values of Re.
Coastal Sediment Properties
III-1-23



 Previous Page
Previous Page
