EM 1110-2-1100 (Part II)
30 Apr 02
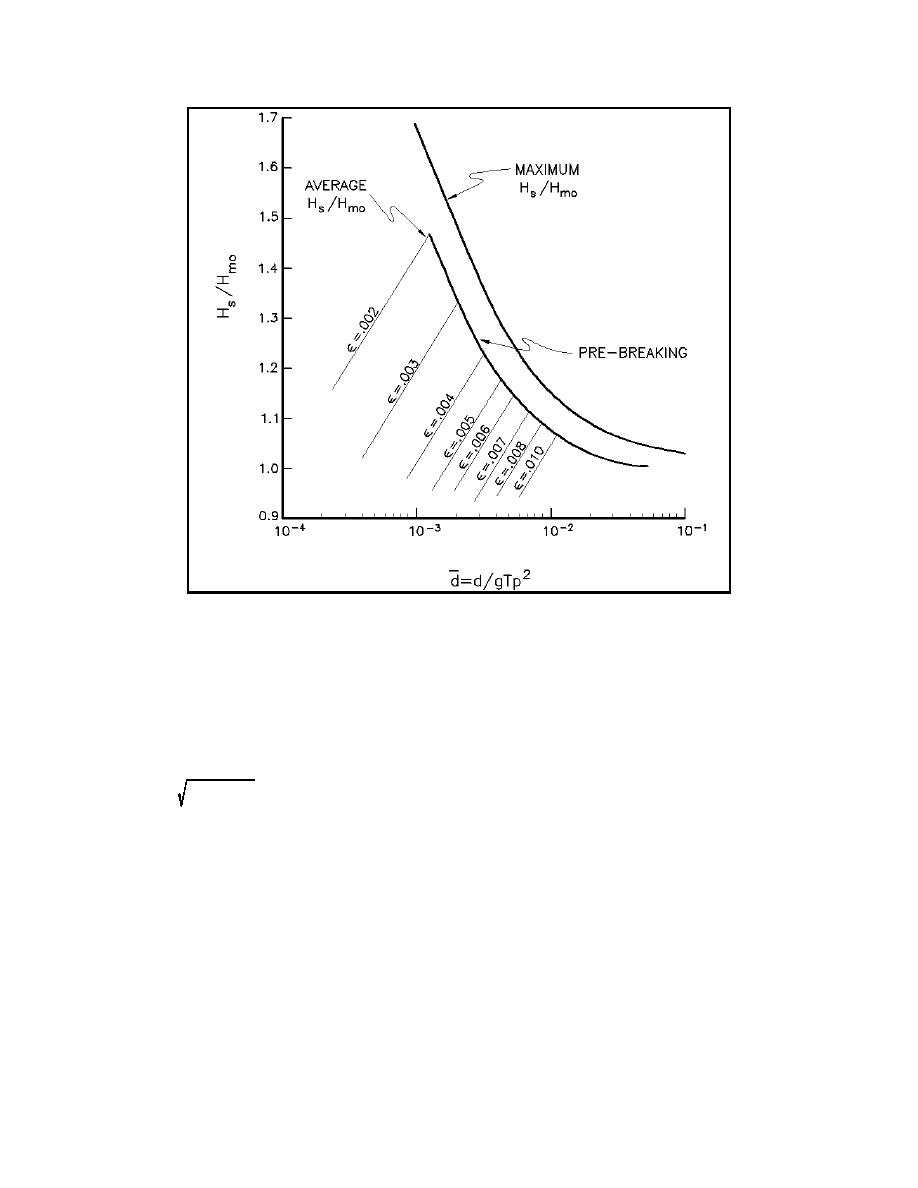
Figure II-1-40. Variation of Hs/Hmo as a function of elative depth d and significant
steepness (Thompson and Vincent 1985)
(h) The parameters λj control the shape and the sharpness of the spectral peak of the Ochi-Hubble
spectral model if in either spectral component (i.e., sea or swell) the values of Hsj and ω0j are held constant.
Therefore, λ1 and λ2 are called the spectral shape parameters. On the assumption of a narrow-bandedness
of the entire Ochi-Hubble spectrum, an equivalent significant wave height may be calculated by
2
2
Hs ' Hs1 % Hs2
(II-1-158)
Note that for λ1 = 1 and λ2 = 0, the PM spectra may be recovered from this equation.
(i) In shallow water, the wave spectrum deviates from the standard spectra forms presented so far, and
at frequencies above the peak, the spectrum no longer decays as f-5. Kitaigorodoskii et al. (1975) showed that
the equilibrium range is proportional to -3 power of the wave number, and thus, the form of the spectrum is
of f-3 in the high-frequency range. This change is attributed to the effect of water depth on wave spectrum
and to the interaction between spectral components. Bouws et al. (1984) proposed a variation to the
JONSWAP energy spectrum for representing wave spectra in finite-depth water. The spectrum so obtained,
the product of JONSWAP and the Kitaigorodoskii depth function accounting for the influence of the water
depth, is called the TMA spectrum after the names of three sources of data used in its development (Texel,
Marsen, and Arsloe).
Water Wave Mechanics
II-1-91




 Previous Page
Previous Page
