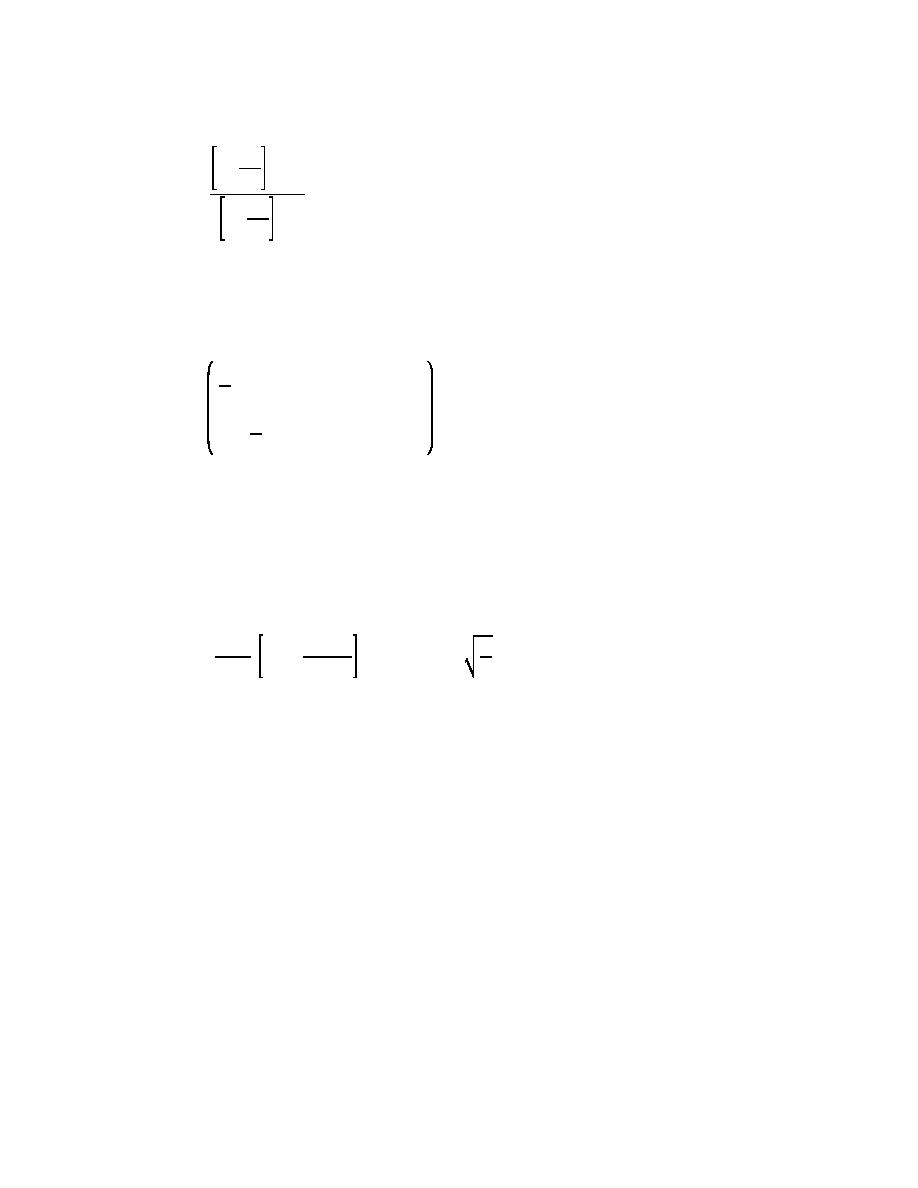
EM 1110-2-1100 (Part II)
30 Apr 02
(j)
Kitaigorodoskii et al. (1975) obtained the form of depth dependence as
Mk
k &3
Mω
d ' finite
Φ(ω, d) '
s
(II-1-159)
Mk
k &3
Mω
d'4
(k) Thus, Φ is a weighing factor of the quantity in the bracket, which is determined from the ratio of
the quantity evaluated for finite and infinite water depth cases. Using the linear wave theory, the above
equation has been approximated by Kitaigorodoskii et. al. (1975) as
1 2
for ω # 1
ω
2
Φ(ω,d) .
(II-1-160)
1
(2 & ω)2
for ω > 1
1&
2
(l) The TMA spectrum was intended for wave hindcasting and forecasting in water of finite depth. This
spectrum is a modification of the JONSWAP spectrum simply by substituting Kitaigorodoskii's expression
for effects of the finite depth equilibrium function. By using the linear wave theory, we find the following
complete form of the TMA spectrum:
STMA(ω,d) ' SJONSWAP(ω) Φ(ω(,d)
1
K
d
(II-1-161)
Φ(ω(,d) '
ω( ' ω
;
1%
sinh K
g
f(ω()
f(ω() ' tanh&1[k(ω()d]
K ' 2ω(2 f(ω()
;
(m) In effect, this substitution transforms the decay or slope of the spectral density function of the
JONSWAP spectrum in the high-frequency side from ω-5 to ω-3 type dependence during the shoaling process
approximated by linear wave theory. Bouws et. al (1984) present equations for α, γ, and σ. As with the
JONSWAP, the equation may be iteratively fit to an observed spectrum and α, γ, fm , and σ may be estimated.
(n) The PM, JONSWAP, and TMA spectra can be estimated if something about the wind, depth and fetch
are known. Furthermore, these spectral equations can be used as target spectra whose parameters can be
varied to fit observed spectra which may have been measured. In the first situation, the value of the
parameterization is in making an educated guess at what the spectrum may have looked like. The value in
the second case is for ease of analytical representation. However, very often today engineering analyses are
made on the basis of numerical simulations of a specific event by use of a numerical model (see Part II-2).
In this case, the model estimates the spectrum and a parametric form is not required.
II-1-92
Water Wave Mechanics




 Previous Page
Previous Page
