EM 1110-2-1100 (Part II)
30 Apr 02
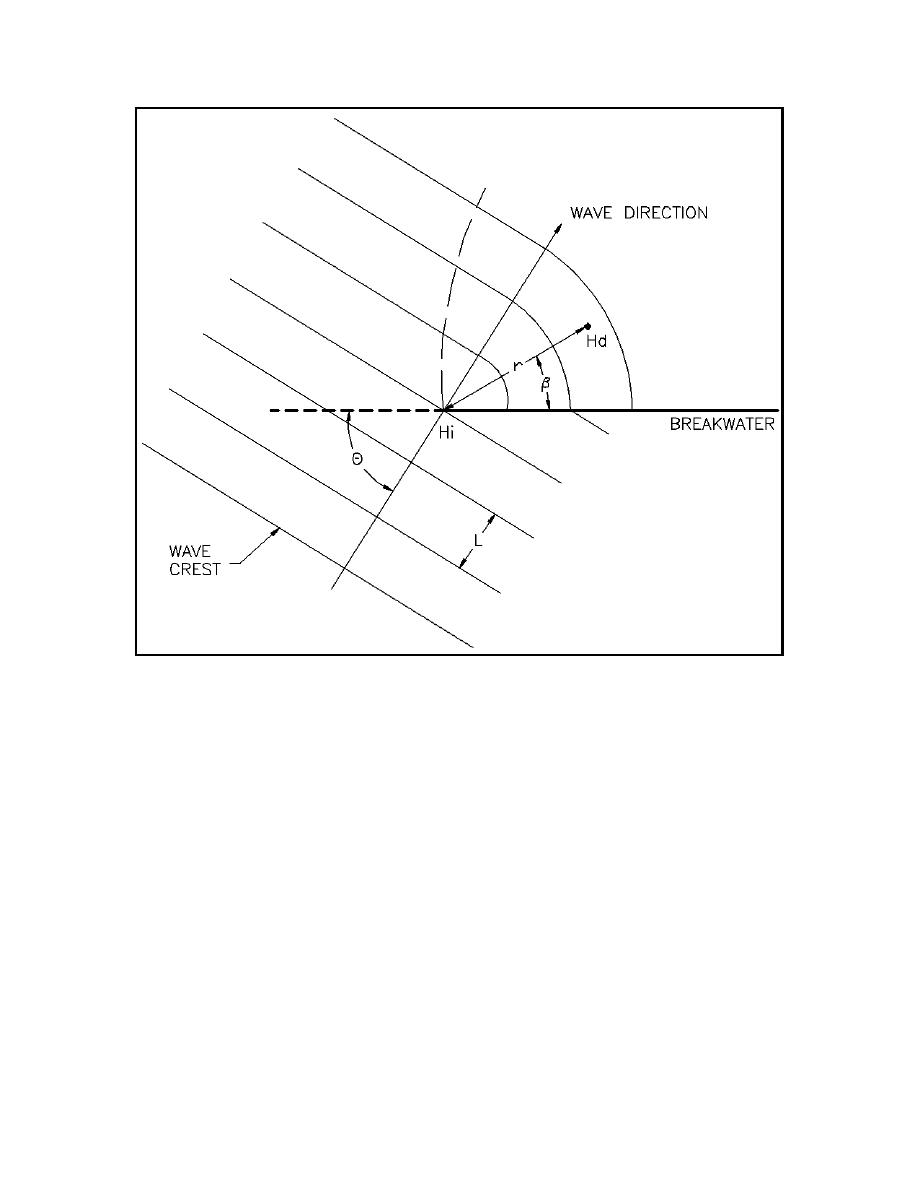
Figure II-7-2.
Wave diffraction, definition of terms
(b) The reflected wave crests (not shown in the figure) would also diffract to form concentric wave crests
that curl around the breakwater tip into the lee. These waves are typically much lower than the incident
waves and are more affected by diffraction when they reach the breakwater lee, so they typically have a very
small height in the lee of the breakwater.
(c) A diffraction coefficient KN = Hd/Hi can be defined where Hd is the diffracted wave height at a point
in the lee of the breakwater and Hi is the incident wave height at the breakwater tip. If r is the radial distance
from the breakwater tip to the point where KN is to be determined and β is the angle between the breakwater
and this radial, then KN = fcn(r/L, β,θ) where θ defines the incident wave direction (see Figure II-7-2) and L
is the wave length. Consequently, for a given location in the lee of the breakwater, the diffraction
coefficient is a function of the incident wave period and direction of approach. So, for a spectrum of incident
waves, each frequency component in the wave spectrum would have a different diffraction coefficient at a
given location in the breakwater lee.
(d) The general problem depicted in Figure II-7-2 was originally solved by Sommerfeld (1896) for the
diffraction of light passing the edge of a semi-infinite screen. Penny and Price (1952) showed that the same
solution applies to the diffraction of linear surface waves on water of constant depth that propagate past the
end of a semi-infinite thin, vertical-faced, rigid, impermeable barrier. Thus, the diffraction coefficients in the
structure lee include the effects of the diffracted incident wave and the much smaller diffracted wave that
II-7-4
Harbor Hydrodynamics




 Previous Page
Previous Page
