EM 1110-2-1100 (Part II)
30 Apr 02
EXAMPLE PROBLEM II-7-1
FIND:
The wave height in the lee of the breakwater at a point specified by β = 30 deg and r = 100 m.
GIVEN:
A train of 6-sec-period 2-m-high waves is approaching a breakwater at an angle θ = 60 deg. The
water depth in the lee of the breakwater is 10 m.
SOLUTION:
From the linear wave theory for a period of 6 sec and a water depth of 10 m, the wave length can
be calculated to be 48.3 m. Thus, r/L = 100/48.3 = 2.07. From Figure II-7-3 at β = 30 deg and r/L =
2.07, KN = 0.28. This yields a diffracted wave height = (0.28)2 = 0.56 m.
The diffracted wave would be propagating in the direction β = 30 deg and would have a continually
diminishing wave height as indicated by Figure II-7-3. If the breakwater has a reflection coefficient that
is less than one, the above result would still be reasonable, since the diffracted height of the reflected
wave would be very small at the point of interest.
(2) Waves passing through a structure gap.
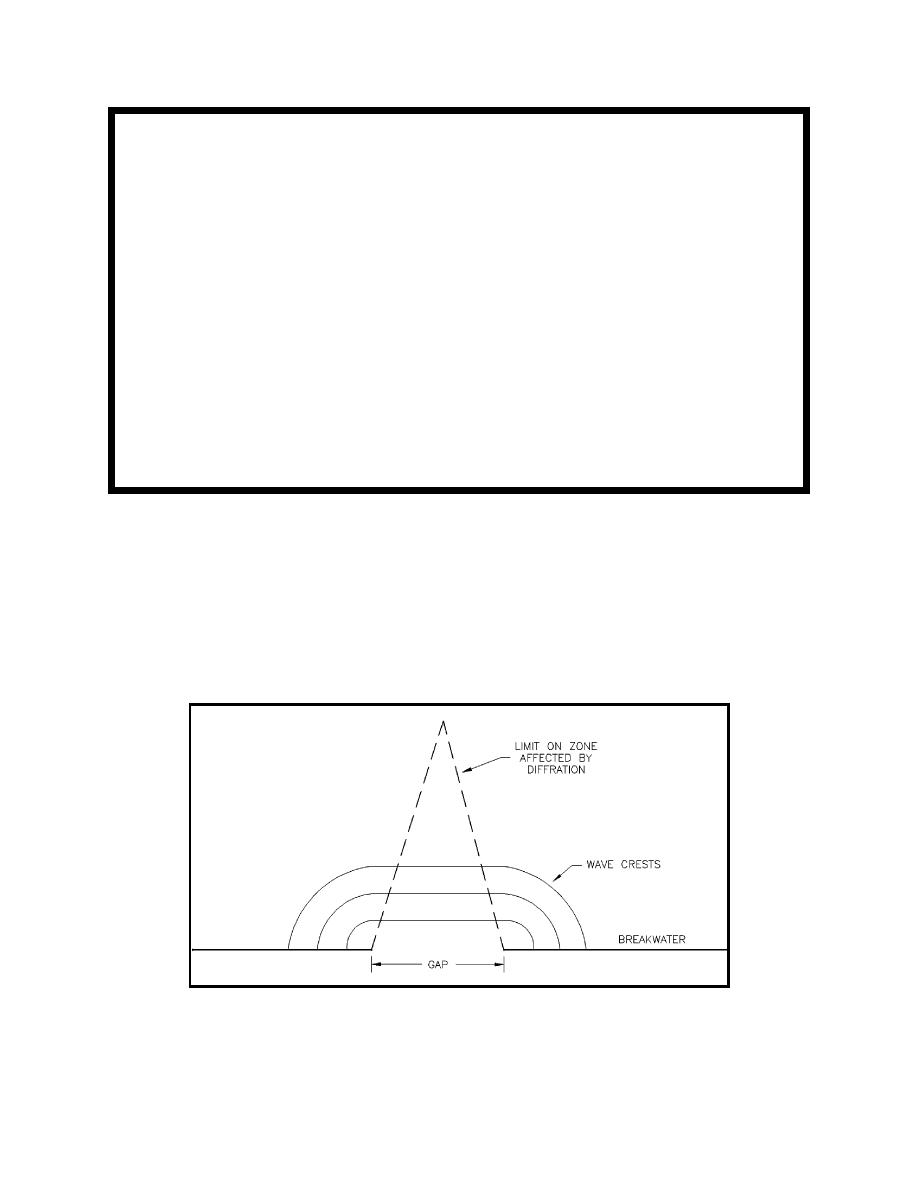
(a) When waves pass through a gap in a breakwater, diffraction occurs in the lee of the breakwater on
both sides of the gap. As the waves propagate further into the harbor, the zone affected by diffraction grows
toward the center line of the gap until the two diffraction zones interact (see Figure II-7-4). The wider the
gap, the further into the harbor this interaction point occurs. For typical harbor conditions and gap widths
greater than about five wavelengths, Johnson (1952) suggests that the diffraction patterns at each side of the
gap opening will be independent of each other and Wiegel (1962) may be referenced for diffraction analysis.
For smaller gap widths, an analysis employing the gap geometry must be used.
Figure II-7-4.
Wave diffraction through a gap
II-7-6
Harbor Hydrodynamics




 Previous Page
Previous Page
