EM 1110-2-1100 (Part II)
30 Apr 02
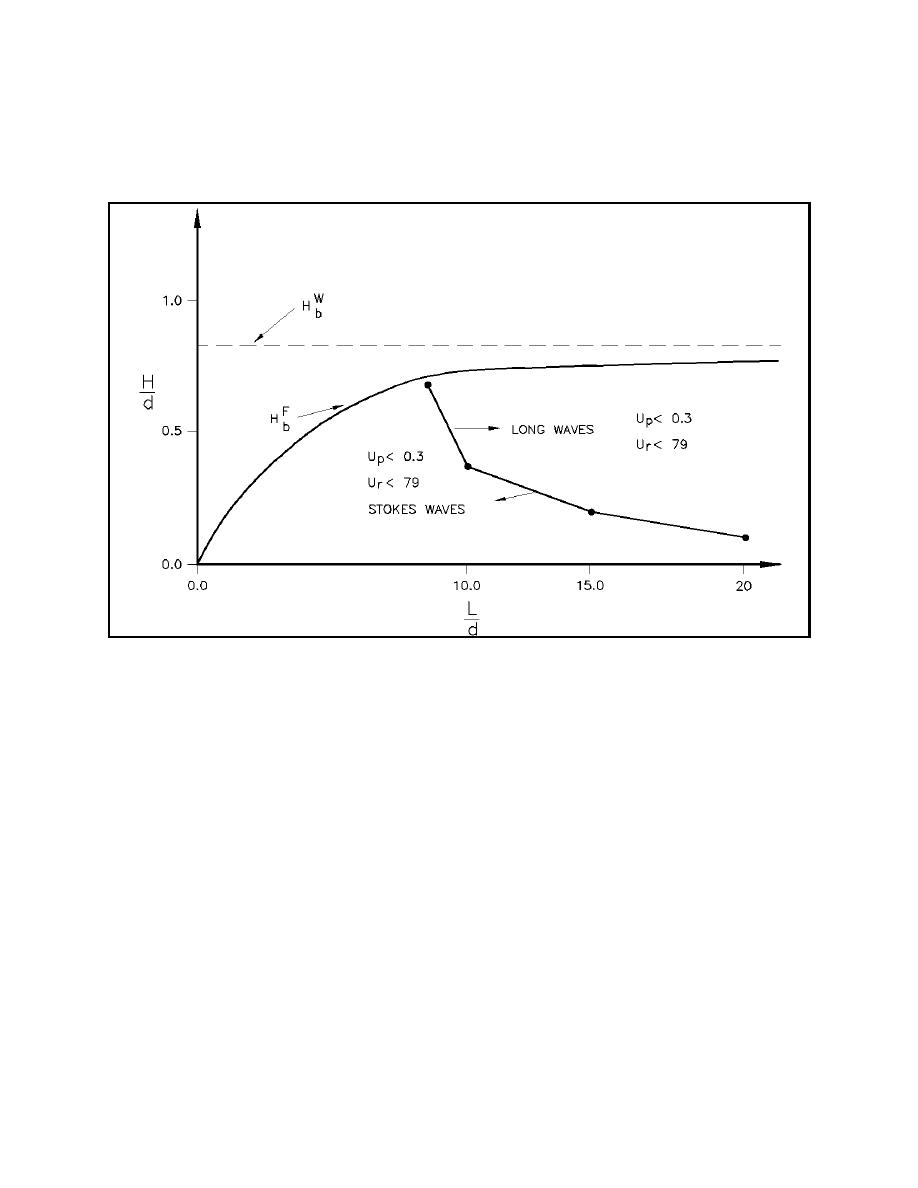
solitary waves (long waves) are valid are also shown in this figure. The breaking limit for solitary waves
HbW = 0.833 established by Williams (1981) and the limiting height designated as HbF determined by Cokelet
(1977) are also shown on Figure II-1-21. The line between short and long waves corresponds to a value of
the Ursell number UR . 79. This theoretical partition agrees with data from Van Dorn (1966).
Figure II-1-21. Grouping of wind waves based on universal parameter and limiting height for steep waves
II-1-3. Irregular Waves
a.
Introduction.
(1) In the first part of this chapter, waves on the sea surface were assumed to be nearly sinusoidal with
constant height, period and direction (i.e., monochromatic waves). Visual observation of the sea surface (as
in the radar image of the entrance to San Francisco Bay in Figure II-1-22) and measurements (such as in
Figure II-1-23) indicate that the sea surface is composed of waves of varying heights and periods moving in
differing directions. In the first part of this chapter, wave height, period, and direction could be treated as
deterministic quantities. Once we recognize the fundamental variability of the sea surface, it becomes
necessary to treat the characteristics of the sea surface in statistical terms. This complicates the analysis but
more realistically describes the sea surface. The term irregular waves will be used to denote natural sea states
in which the wave characteristics are expected to have a statistical variability in contrast to
monochromatic waves, where the properties may be assumed constant. Monochromatic waves may be
generated in the laboratory but are rare in nature. "Swell" describes the natural waves that appear most like
monochromatic waves in deep water, but swell, too, is fundamentally irregular in nature. We note that the
sea state in nature during a storm is always short-crested and irregular. Waves that have travelled far from
Water Wave Mechanics
II-1-59



 Previous Page
Previous Page
