EM 1110-2-1100 (Part II)
30 Apr 02
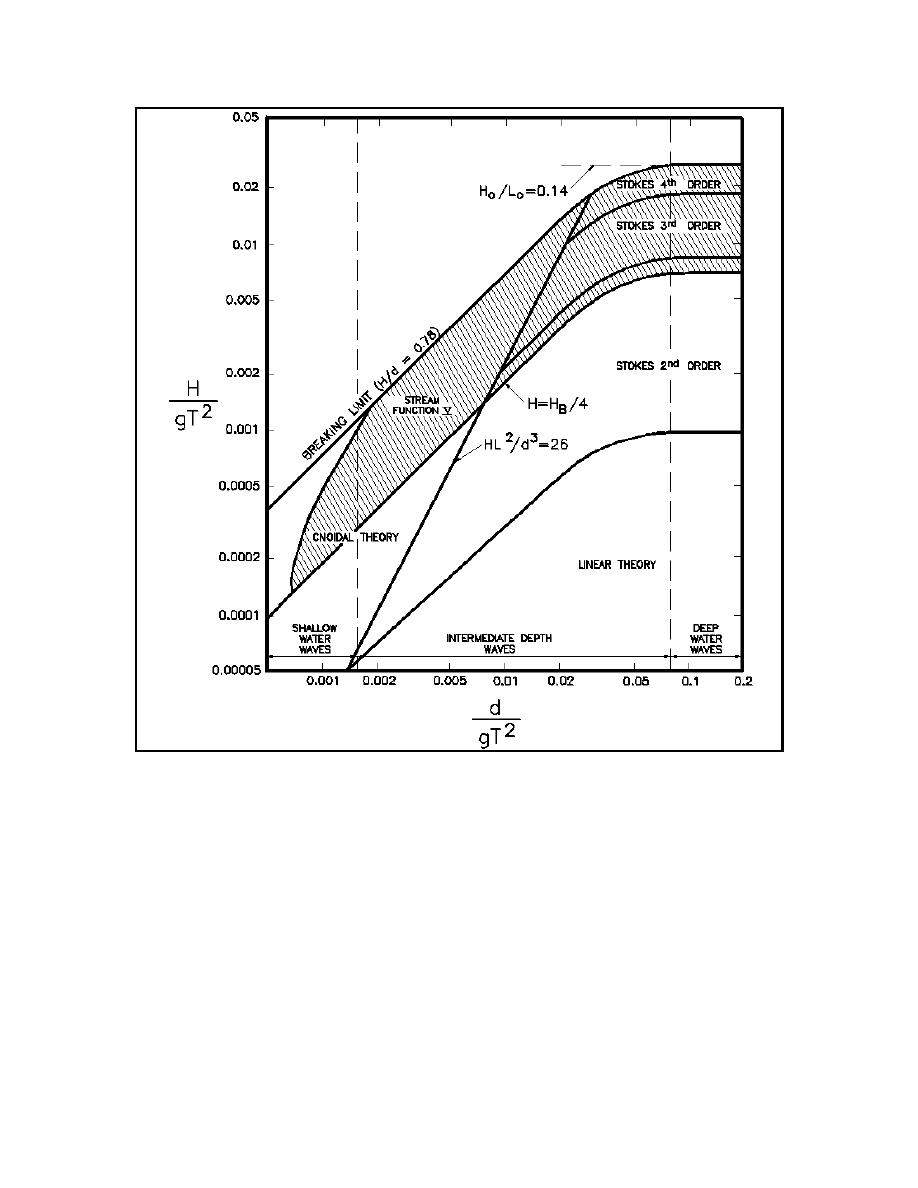
Figure II-1-20. Ranges of suitability of various wave theories (Le Mhaut 1976)
(6) Similarly, using the fifth-order expansion, the asymptotes to Stokes third-order theory are H/L0 <
0.1 and H/d < 3/4(kd)2 for deep water and shallow water, respectively. This allows the range of Stokes'
theory to be expanded by adding successively smaller areas to the domain of linear theory in Figure II-1-20
until the breaking limit is reached. The fifth-order Stokes theory gets close enough to the breaking limit, and
higher order solutions may not be warranted. Laitone (1962) suggests a shallow-water limit on Stokes' theory
by setting the Ursell number UR equal to 20. For an Ursell number of approximately 20, Stokes' theory
approaches the cnoidal theory.
Figure II-1-20 may be used to establish the boundaries of regions where a particular wave theory should be
used. Stokes (1847) noted that this parameter should be small for long waves. An alternative, named the
Universal parameter (Up), has recently been suggested (Goda 1983) for classification of wave theories.
(8) Limits of validity of the nonlinear (higher-order) wave theories established by Cokelet (1977) and
Williams (1981), are shown in Figure II-1-21. Regions where Stokes waves (short waves) and cnoidal and
II-1-58
Water Wave Mechanics



 Previous Page
Previous Page
