Figure II-1-41. Identification and description of wave groups through ordered statistics (Goda 1976)

Part-II-Chap1
Page Navigation
96

EM 1110-2-1100 (Part II)

30 Apr 02

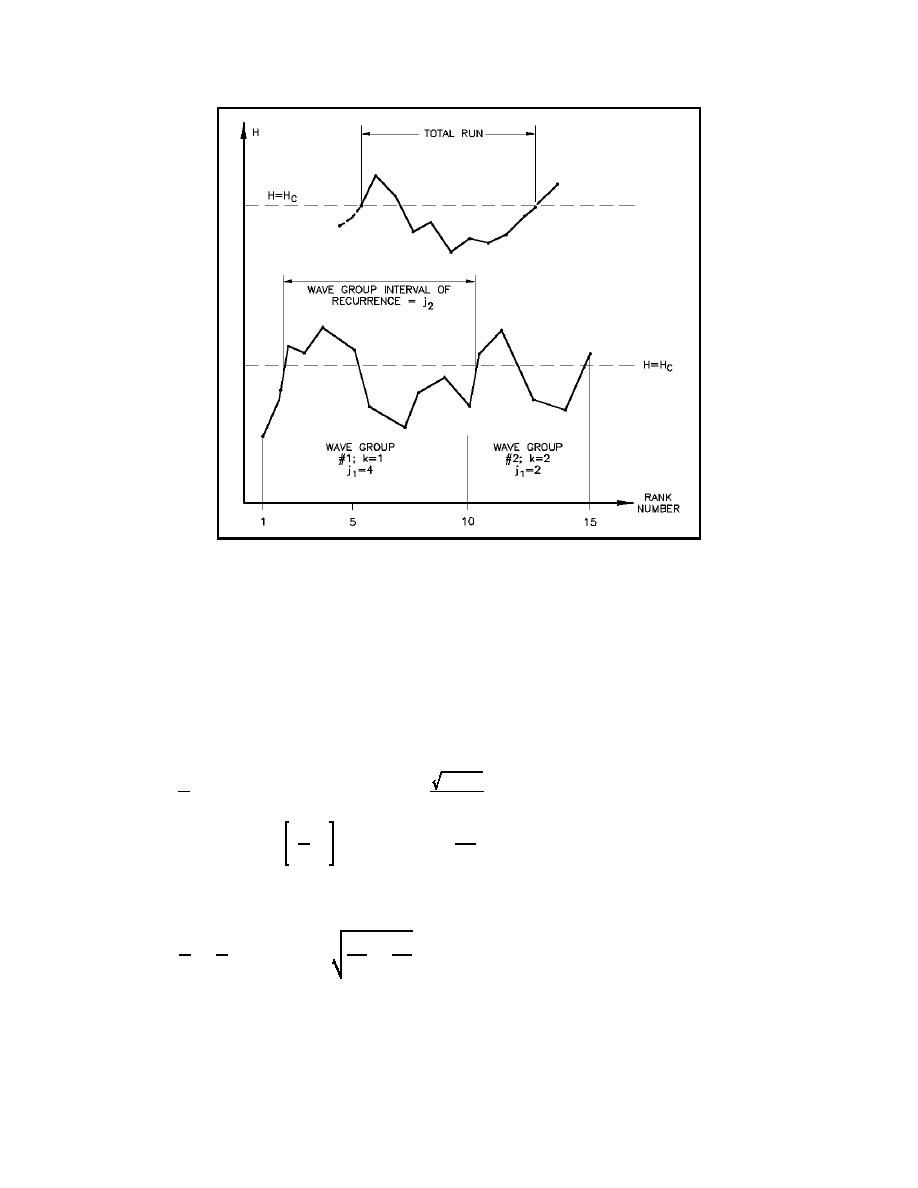
Figure II-1-41. Identification and description of wave groups through

ordered statistics (Goda 1976)

(f)

Assuming that successive wave heights are uncorrelated, the probability of a run length j1 is (Goda

1976)

(j1&1)

P(j1) ' p

(II-1-170)

(1&p)

in which p is the occurrence probability for H > Hc. The mean and standard deviation of j1 are

1&q

;

q'1&p

;

σj '

j '

(II-1-171)

p ' p(H>Hc) ' exp & ηc2

;

ηc'

ση

(g) The probability of a total run with the length j2 can be derived by mathematical induction as

j '

(II-1-172)

;

σj '

where it has been assumed that successive wave heights are uncorrelated. Successive wave heights of the real

ocean waves are mutually correlated, and the degree of correlation depends on the sharpness of the spectral

peak. The effect of spectral bandwidth on wave height distribution has been considered by Kimura (1980),

Tayfun (1983a), and Longuet-Higgins (1984). Tayfun has shown that the parameter that best describes the

II-1-96

Water Wave Mechanics