EM 1110-2-1100 (Part II)
30 Apr 02
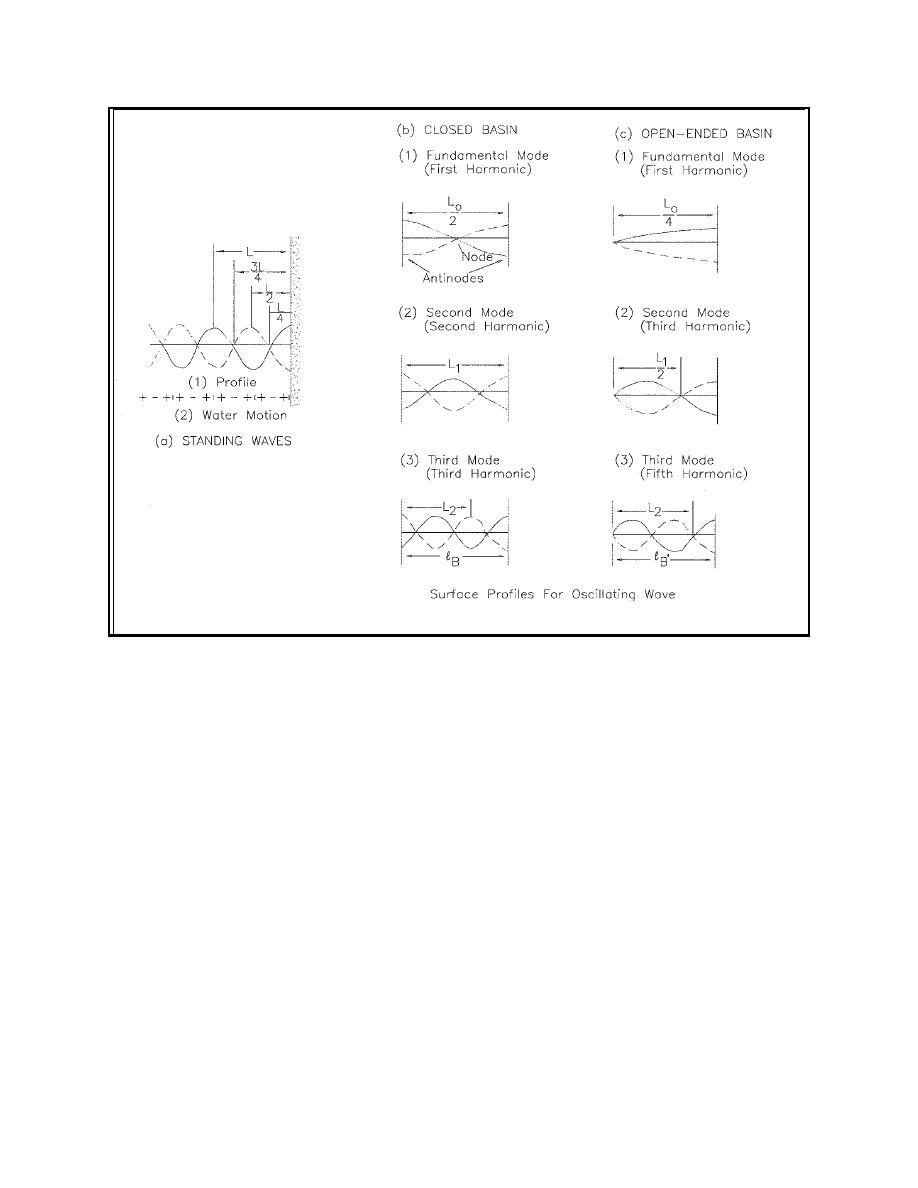
Figure II-5-30.
Long wave surface profiles (Shore Protection Manual 1984)
f.
Methods are available to estimate free oscillations in long narrow lakes of variable width and depth
(Defant 1961); however, seiche periods and node/antinode locations are determined most accurately through
long-wave modeling. For this class of problem, numerical solutions of the governing equations are necessary.
An example is presented in Rao and Schwab (1976), in which a numerical model is used to investigate the
normal modes of oscillation in an arbitrary enclosed basin on a rotating earth. Applications are made to Lakes
Ontario and Superior. Rao and Schwab describe two distinct types of free oscillations, gravitational modes
and rotational modes. Gravitational modes result from undulations of the free surface and are independent
of the rotation of the earth. Rotational modes are a function of gravity via the Coriolis parameter. Figure II-
5-31 represents the first, second, and third normal modes of oscillation for Lake Ontario. The periods of the
computed six lowest modes in Lake Ontario are 5.11, 3.11, 2.13, 1.87, 1.78, and 1.46 hr for modes 1 through
6. The complexity of the nodal points and lines of phase demonstrate that idealized solutions such as those
shown in Figure II-5-30 are often not adequate to explain natural phenomena. For applications requiring
detailed information on maximum seiche elevations and nodal distributions, numerical models such as those
described in the following section are the only viable approach to developing reliable solutions.
Water Levels and Long Waves
II-5-53



 Previous Page
Previous Page
