EM 1110-2-1100 (Part II)
30 Apr 02
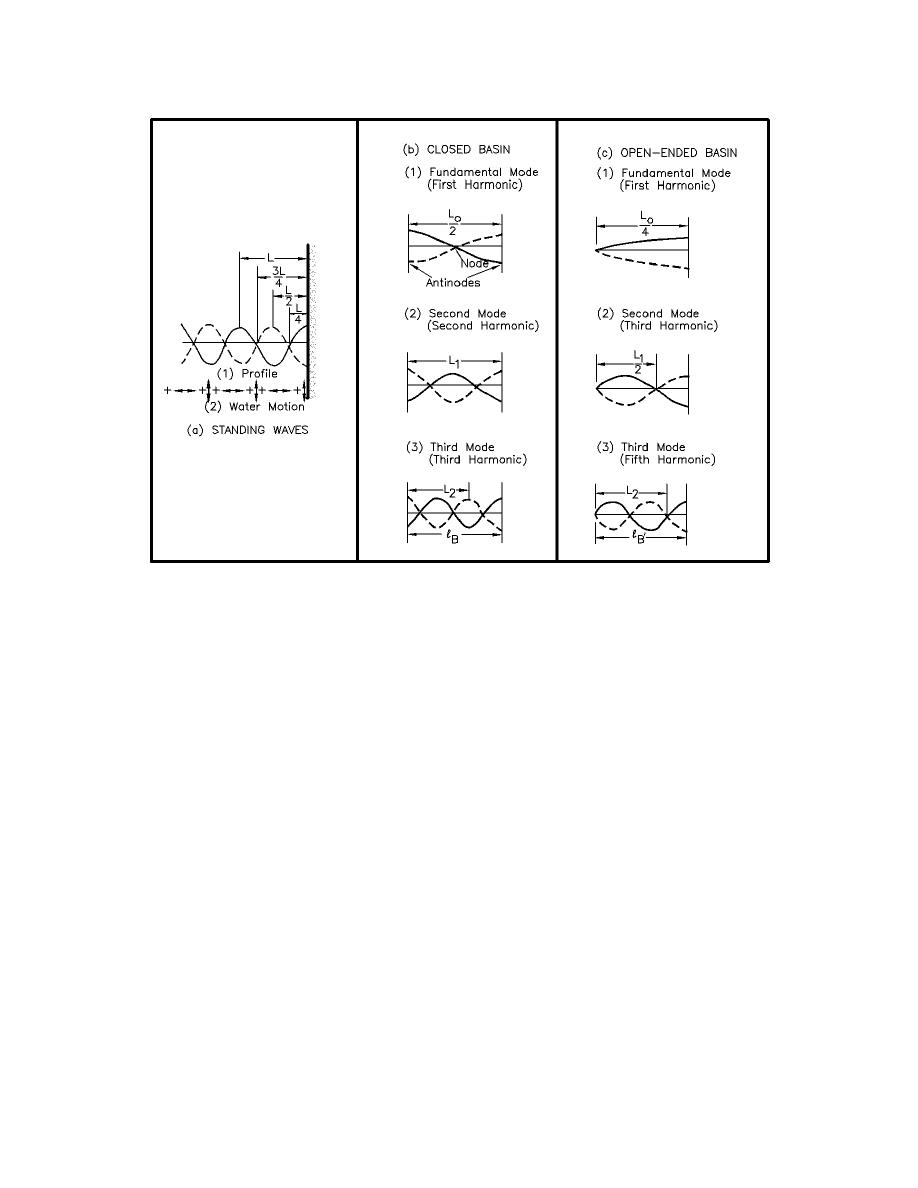
Figure II-7-26.
Surface profiles for oscillating waves (Carr 1953)
b. Mechanical analogy.
(1) The basic theory for basin oscillations is similar to that of free and forced oscillations experienced
by some mechanical, acoustical, and other fluid systems. Certain systems respond to a disturbance by
developing a restoring force that reestablishes equilibrium in the system. A pendulum is a good example of
such a system. A free oscillation at the system's natural period or frequency is initiated if the system is carried
by inertia beyond the equilibrium condition. If the forces responsible for the initial disturbance are not
sustained, free oscillations at the natural frequency will continue, but their amplitude decays exponentially
due to friction. The system eventually comes to rest. Forced oscillations can occur at non-natural frequencies
if cyclic energy is applied to a system at non-natural frequencies. Continuous excitation at frequencies at or
near the natural frequency of a system generally causes an amplified response. The response magnitude
depends on the proximity of the excitation to the natural frequency and the frictional characteristics of the
system.
(2) The response of a linearly damped, vibrating spring-mass system with one degree of freedom
provides a good illustration (Figure II-7-27). Terms are defined as follows: A = amplification factor (ratio
of mass displacement to excitation displacement); T = excitation (and response) period; Tn = natural period
of the mass-spring system; and φ = phase angle by which the mass displacement lags the excitation
displacement. The mass responds directly to the excitation if the excitation period is much greater than the
natural period of the system; that is, A = 1 and φ = 0E when Tn/T << 1. The harbor equivalence to this case
is the harbor response to astronomical tides. The mass responds very little and out of phase with the
excitation if the excitation period is much shorter than the natural period of the system; that is, A << 1 and
φ 180E when Tn/T >> 1. The mass response is amplified and a phase lag develops as the excitation period
approaches the natural period of the system. The ratio Tn/T determines the degree of amplification and phase
Harbor Hydrodynamics
II-7-33



 Previous Page
Previous Page
