EM 1110-2-1100 (Part III)
30 Apr 02
is homogeneous, that is, the empirical proportionality coefficient K is dimensionless. This is another
advantage in using IR rather than the QR volume transport rate. Equation 2-5 is commonly referred to as the
"CERC formula."
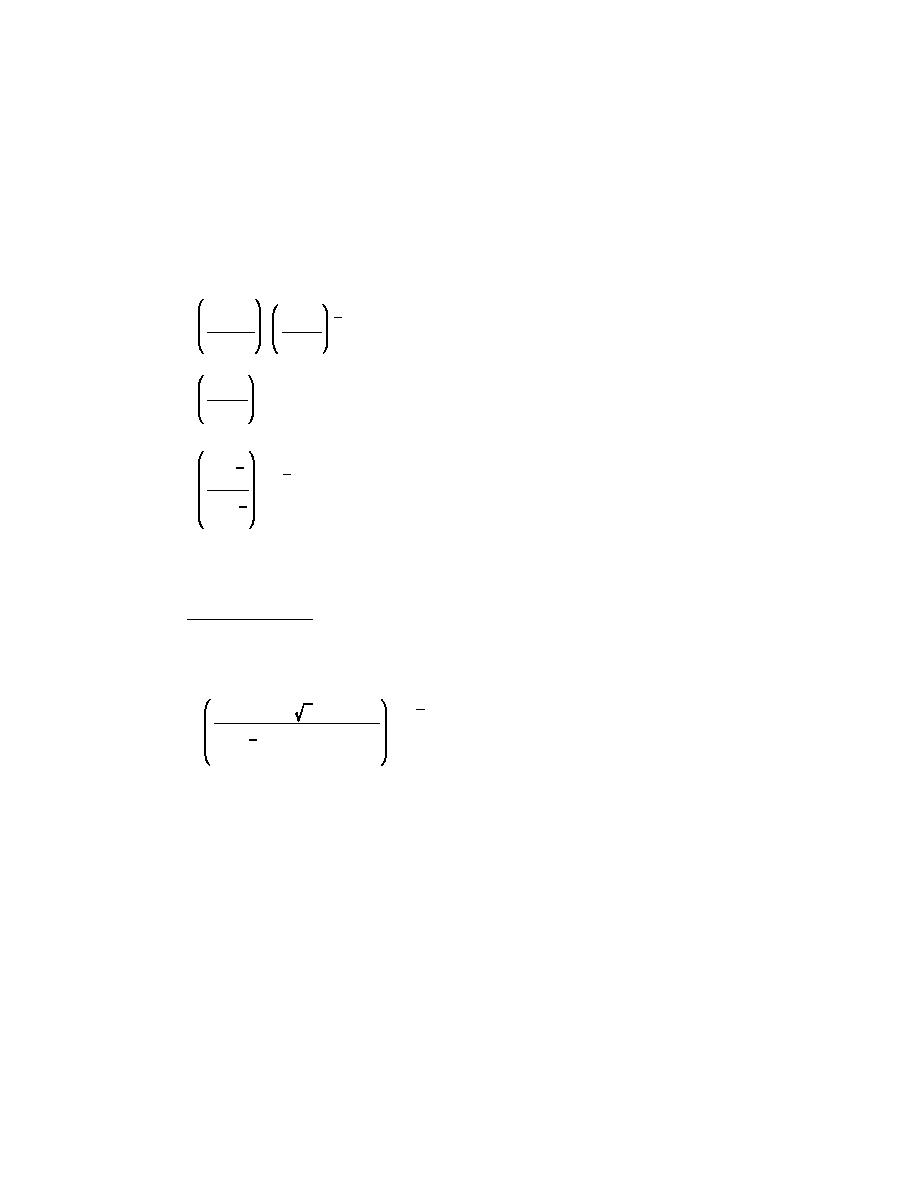
(b) Equation 2-5 may be written
IR ' K PR ' K (E Cg)b sinαb cosαb
(III-2-6a)
which, on assuming shallow water breaking, gives
1
2
ρ g Hb
g Hb
(III-2-6b)
2
IR ' K
sinαb cosαb
8
κ
ρ g 3/2
5/2
IR ' K
Hb
sinαb cosαb
(III-2-6c)
8 κ1/2
3
5
2
ρg
2
IR ' K
Hb
sin(2αb)
(III-2-6d)
1
2
16 κ
(c) By using Equation 2-1b, the relationships for IR can be converted to a volume transport rate:
K
QR '
P
(III-2-7a)
(ρs & ρ) g (1 & n) R
5
ρ g
2
Hb
QR ' K
sin (2αb)
(III-2-7b)
1
2
16 κ (ρs & ρ) (1 & n)
(d) Field data relating IR and PR are plotted in Figure III-2-4, for which the calculations of the wave power
are based on the root-mean-square (rms) wave height at breaking Hb rms . Data presented in Figure III-2-4
include those measured by: (1) sand accumulation at jetties and breakwaters (South Lake Worth Inlet, Florida
(Watts 1953a); Anaheim Bay (Caldwell 1956), Santa Barbara (Dean et al. 1987), and Channel Islands (Bruno
et al. 1981, Walton and Bruno 1989), California; Rudee Inlet, Virginia (Dean et al. 1987); Cape Thompson,
Alaska (Moore and Cole 1960); and Point Sapin, Canada (Kamphuis 1991)); (2) sand tracer at Silver Strand,
California (Komar and Inman 1970); El Moreno, Mexico (Komar and Inman 1970); Torrey Pines, California
(Inman et al. 1980); and Ajiguara, Japan (Kraus et al. 1982)); and (3) sediment traps at Kewaunee County,
Wisconsin (Lee 1975); and Duck, North Carolina (Kana and Ward 1980)). Because of questions in
methodologies and trapping efficiencies, probably the data sets most appropriate for engineering application
are those based upon category 1 above, sand accumulation (impoundment) at jetties and breakwaters.
Longshore Sediment Transport
III-2-11



 Previous Page
Previous Page
