Wave transformation procedure.

Part_III-Chap_2
Page Navigation
21

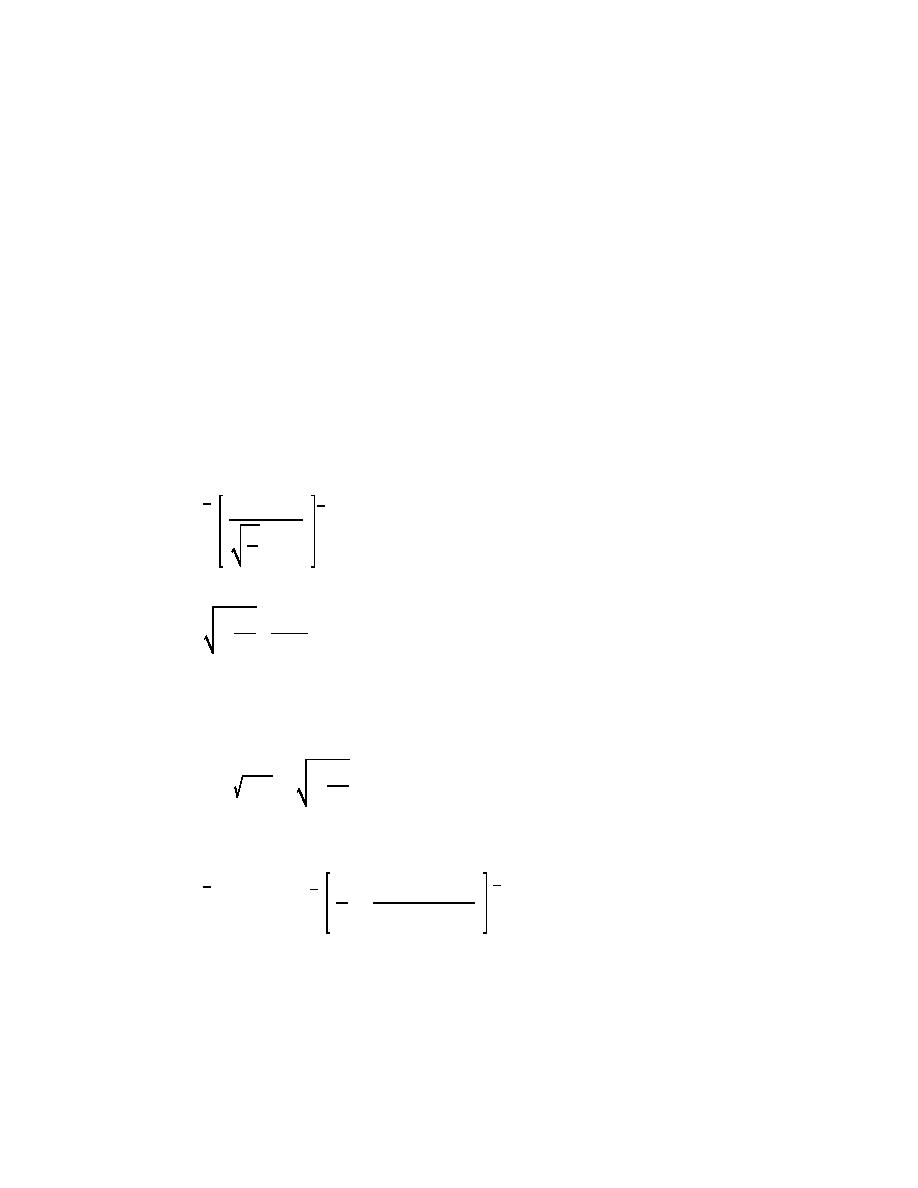
EM 1110-2-1100 (Part III)

30 Apr 02

and more accurate to measure the longshore current VR than it is to determine the breaker angle αb needed in

the PR formulation. In either method, calculations of longshore sediment transport may be very different than

actual values. Formulations for the longshore current distribution across nonplanar, concave-up beach

profiles are presented by McDougal and Hudspeth (1983a, 1983b, and 1989) and by Bodge (1988).

c. Using hindcast wave data. Potential longshore sand transport rates can be calculated using Wave

Information Study (WIS) hindcast wave estimates (see Part II-2). First, refraction and shoaling of incident

linear waves are calculated using Snell's law and the conservation of wave energy flux. The shallow-water

wave breaking criterion then defines wave properties at the break point, and potential longshore sand

transport rates are calculated by means of the energy flux method.

(1) Wave transformation procedure. To calculate the potential longshore sand transport rate using

Equation 2-7b, the breaking wave height and incident angle with respect to the shoreline are required. WIS

hindcast estimates, however, are given for intermediate to deepwater depths (Hubertz et al. 1993). Refraction

and shoaling transformation of the WIS hindcast wave estimates to breaking conditions are therefore

necessary and can be accomplished using linear wave theory for coastlines having reasonably straight and

parallel bottom contour lines. Assuming that offshore depth contours are straight and parallel to the trend

of the shoreline and neglecting energy dissipation prior to breaking, the wave height and angle at breaking

can be computed from the coupled equations

Cg1 cosα1

Hb '

(III-2-13)

cosαb

sinα1

sinαb '

(III-2-14)

where the subscript "1" refers to offshore (WIS) conditions. Equations 2-13 and 2-14 are derived from energy

conservation and Snell's Law. Where it is assumed that wave breaking occurs for shallow-water wave

conditions; i.e.,

(III-2-15)

Cb ' Cgb ' g db '

Employing the identity sin2αb = 1 - cos2αb, Equations 2-13 and 2-14 can be combined as

Hb g 2 sin2(α1)

H1 (

Cg1 cos α1 )

Hb '

(III-2-16)

and solved iteratively for Hb. The angle αb can then be found using Equation 2-14. In application of

Equations 2-14 and 2-16, the offshore wave angle α1 should be transformed relative to the shoreline-

perpendicular as described below.

Longshore Sediment Transport

III-2-21