EM 1110-2-1100 (Part III)
30 Apr 02
Example Problem III-2-7 (Concluded)
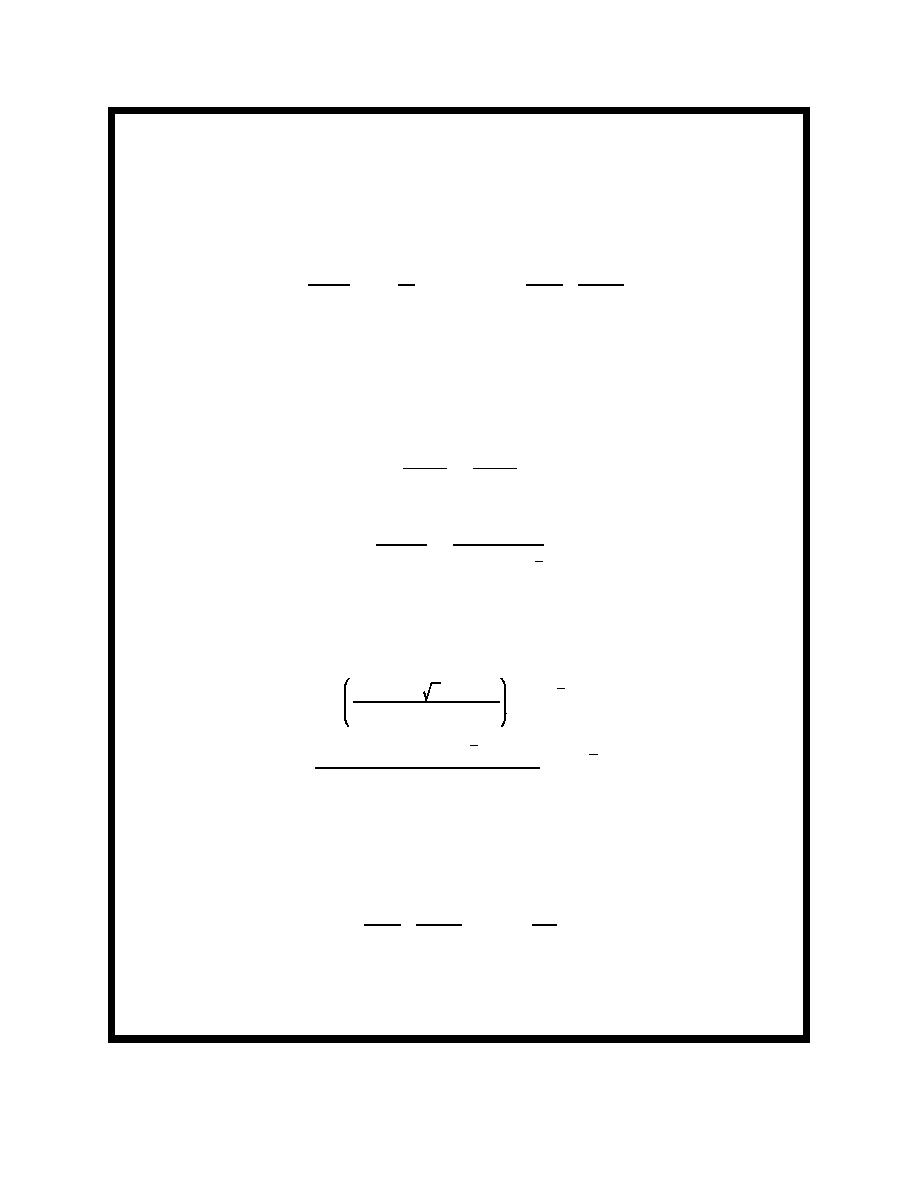
For some applications, such as weir design, only the percentage of longshore transport in a given
region of the surf zone is of interest, and determination of the dimensional normalizing constant kq
may not be necessary. However, kq may be calculated by integrating qx(y)/kq across the surf zone,
determined here by calculating the area below the points in Figure III-2-22b
yb
260
qx (y)
kg m 2
1
9300
m kq
kq m
qx (y) dy .
dy '
kq
sec4
ys
106
where ys is the cross-shore coordinate at the start of the surf zone, (approximately 106 m) and yb is
the cross-shore coordinate at the breaker line (the breaking wave height of 2.42 m occurs at 260 m).
Next, the total longshore sand transport rate is calculated. The offshore wave celerity may be
calculated using linear wave theory as Cg1 = 9.0 m/sec. Breaking wave angle may be calculated
using Snell's Law (Equation 6-13) with input wave conditions (α1 = 10o, d1 = 10 m) and a depth at
breaking = 3.2 m
sin α1
sin αb
'
Cg1
Cgb
sinαb
sin 10o
'
9.0
1
2
(9.81 (3.2))
αb ' 6.2o
The total longshore transport rate may be calculated using Equation 2-7b where K = 0.60
5
ρ g
2
Hb rms
QR ' K
sin(2αb)
16 κ (ρs & ρ)(1 & n)
1
5
2
(1025) (9.81)
(2.42) 2 sin(2(6.2o))
QR ' 0.60
16 (1) (2650 & 1025) (1 & 0.4)
QR = (0.242 m3/sec) (3600 sec/hr) (24 hr/day)
QR = 20.9 x 103 m3/day (27.3 x 103 yd3/day)
The value of kq may be calculated
kg m 2
m3
9300
' 0.242
sec
kq
4
sec
Therefore, kq ~ 38,000 sec3/kg, and the transport rates in Figure III-2-22b and the table can be converted
to values of qx(y) (units m3/sec/m), if desired.
Example Problem III-2-7 (Sheet 4 of 4)
Longshore Sediment Transport
III-2-47



 Previous Page
Previous Page
