EM 1110-2-1100 (Part II)
30 Apr 02
L
C'
(II-1-7)
T
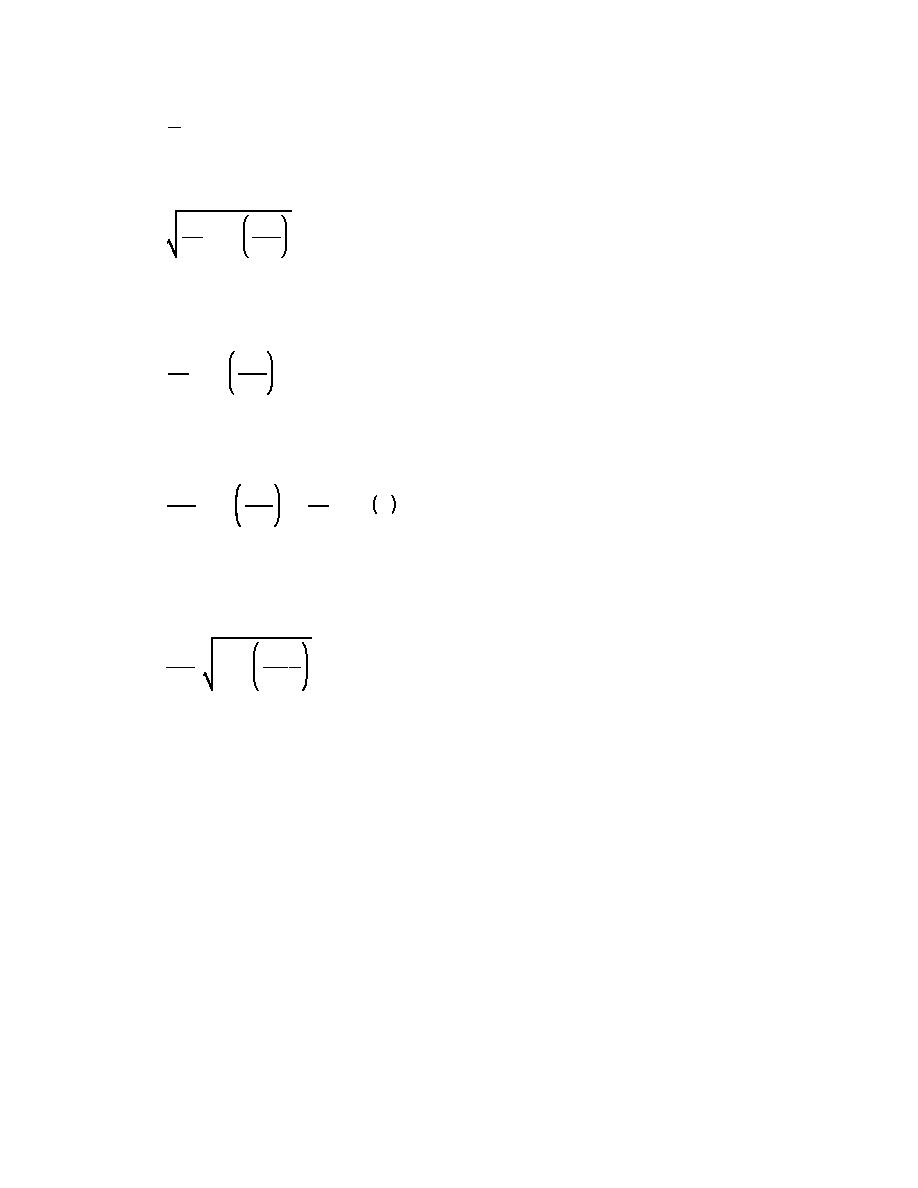
(b) An expression relating wave celerity to wavelength and water depth is given by
gL
2πd
C'
(II-1-8)
tanh
2π
L
(c) Equation II-1-8 is termed the dispersion relation since it indicates that waves with different periods
travel at different speeds. For a situation where more than one wave is present, the longer period wave will
travel faster. From Equation II-1-7, it is seen that Equation II-1-8 can be written as
gT
2πd
tanh
C'
(II-1-9)
2π
L
(d) The values 2π/L and 2π/T are called the wave number k and the wave angular frequency ω,
respectively. From Equation II-1-7 and II-1-9, an expression for wavelength as a function of depth and wave
period may be obtained as
gT 2
2πd
gT
tanh
tanh kd
L'
(II-1-10)
'
2π
L
ω
(e) Use of Equation II-1-10 involves some difficulty since the unknown L appears on both sides of the
equation. Tabulated values of d/L and d/L0 (SPM 1984) where L0 is the deepwater wavelength may be used
to simplify the solution of Equation II-1-10. Eckart (1952) gives an approximate expression for Equa-
tion II-1-10, which is correct to within about 10 percent. This expression is given by
gT 2
4π2 d
L.
tanh
(II-1-11)
2π
T2 g
(f) Equation II-1-11 explicitly gives L in terms of wave period T and is sufficiently accurate for many
engineering calculations. The maximum error 10 percent occurs when d/L . 1/2. There are several other
approximations for solving Equation II-1-10 (Hunt 1979; Venezian and Demirbilek 1979; Wu and Thornton
1986; Fenton and McKee 1990).
(g) Gravity waves may also be classified by the water depth in which they travel. The following
classifications are made according to the magnitude of d/L and the resulting limiting values taken by the
function tanh (2πd/L). Note that as the argument of the hyperbolic tangent kd = 2πd/L gets large, the tanh (kd)
approaches 1, and for small values of kd, tanh (kd) . kd.
(h) Water waves are classified in Table II-1-1 based on the relative depth criterion d/L.
Water Wave Mechanics
II-1-7



 Previous Page
Previous Page
