EM 1110-2-1100 (Part II)
30 Apr 02
EXAMPLE PROBLEM II-1-2
FIND:
The local horizontal and vertical velocities u and w, and accelerations αx and αz at an elevation z = -5 m (or
z = -16.4 ft) below the SWL when θ = 2πx/L - 2πt/T = π/3 (or 600).
GIVEN:
A wave with a period T = 8 sec, in a water depth d = 15 m (49 ft), and a height H = 5.5 m (18.0 ft).
SOLUTION:
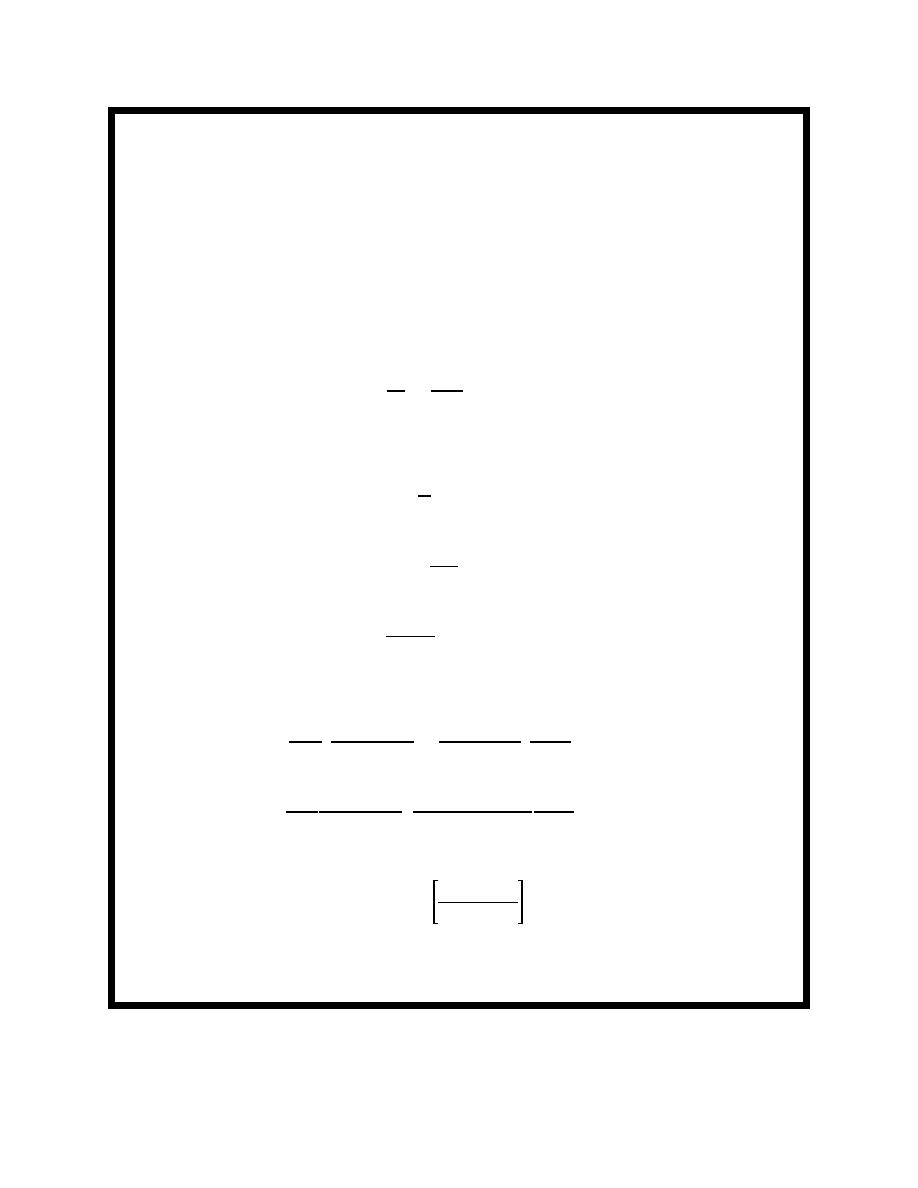
Calculate
L0 ' 1.56T 2 ' 1.56(8)2 ' 99.8 m (327 ft)
d
15
' 0.1503
'
L0
99.8
By trial-and-error solution or using Figure II-1-5 for d/L0 = 0.1503, we find
d
' 0.1835
L
and
2πd
cosh
' 1.742
L
hence
15
' 81.7 m (268 ft)
L'
0.1835
Evaluation of the constant terms in Equations II-1-22 to II-1-25 gives
HgT
1
5.5 (9.8)(8)
1
' 1.515
'
2L cosh(2πd/L)
2 (81.7) 1.742
Hgπ
1
5.5 (9.8)(3.1416) 1
' 1.190
'
L cosh(2πd/L)
81.7
1.742
Substitution into Equation II-1-22 gives
2π(15 & 5)
[cos 600]
u ' 1.515 cosh
81.7
' 1.515 [cosh(0.7691)] (0.500)
Example Problem II-1-2 (Continued)
Water Wave Mechanics
II-1-15



 Previous Page
Previous Page
