EM 1110-2-1100 (Part II)
30 Apr 02
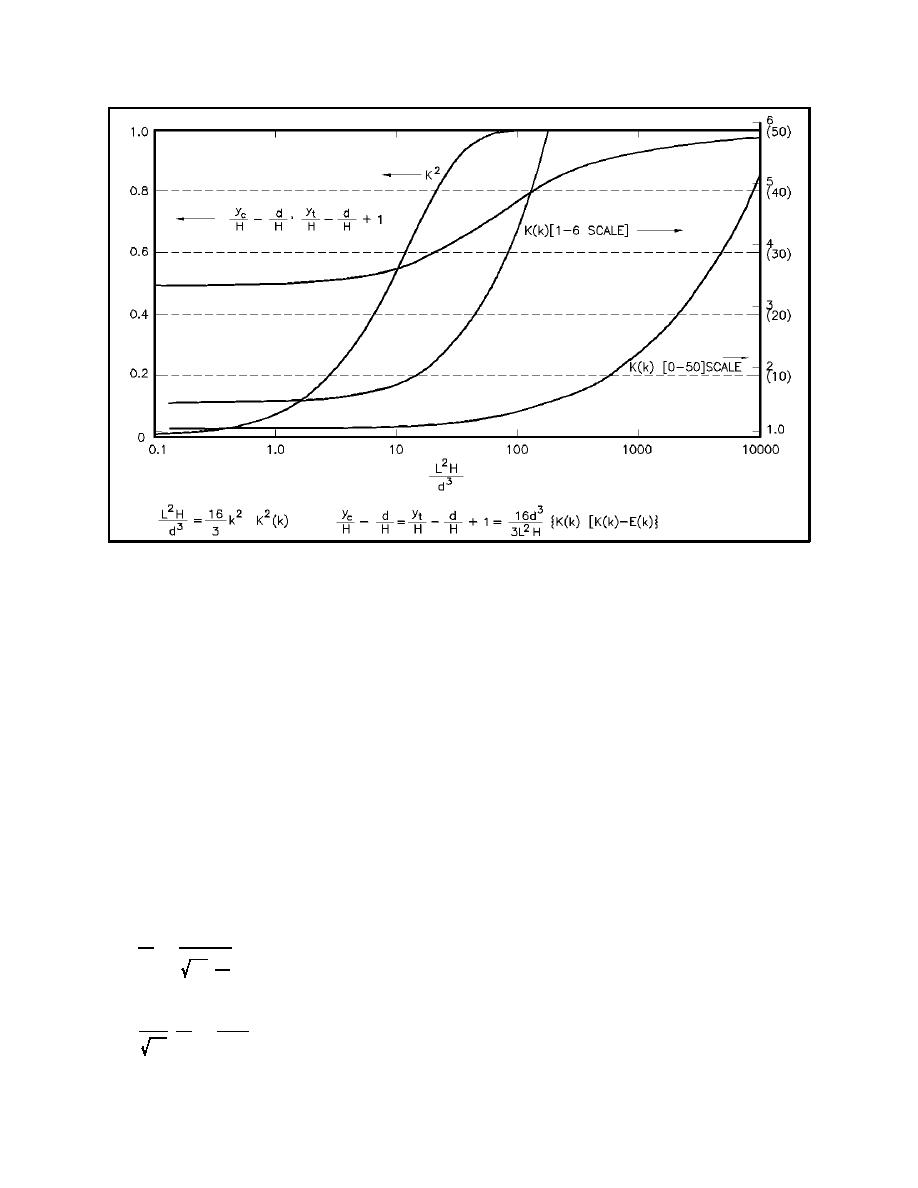
Figure II-1-14. Relationship among L2H/d3 and the square of the elliptic modulus (k2), yc/H, yt/H, and K(k)
(Wiegel 1960)
of solitary waves were performed by Fenton (1972), Longuet-Higgins and Fenton (1974), and Byatt-Smith
and Longuet-Higgins (1976). The first systematic observations and experiments on solitary waves can
probably be attributed to Russell (1838, 1844), who first recognized the existence of a solitary wave.
(c) In nature it is difficult to form a truly solitary wave, because at the trailing edge of the wave there
are usually small dispersive waves. However, long waves such as tsunamis and waves resulting from large
displacements of water caused by such phenomena as landslides and earthquakes sometimes behave
approximately like solitary waves. When an oscillatory wave moves into shallow water, it may often be
approximated by a solitary wave (Munk 1949). As an oscillatory wave moves into shoaling water, the wave
amplitude becomes progressively higher, the crests become shorter and more pointed, and the trough becomes
longer and flatter.
(d) Because both wavelength and period of solitary waves are infinite, only one parameter H/d is needed
to specify a wave. To lowest order, the solitary wave profile varies as sech2q (Wiegel 1964), where q =
(3H/d)1/2 (x-Ct)/2d and the free-surface elevation, particle velocities, and pressure may be expressed as
η
u
(II-1-83)
'
H
H
gd
d
u
H
∆p
(II-1-84)
'
gd d
ρgH
II-1-42
Water Wave Mechanics



 Previous Page
Previous Page
