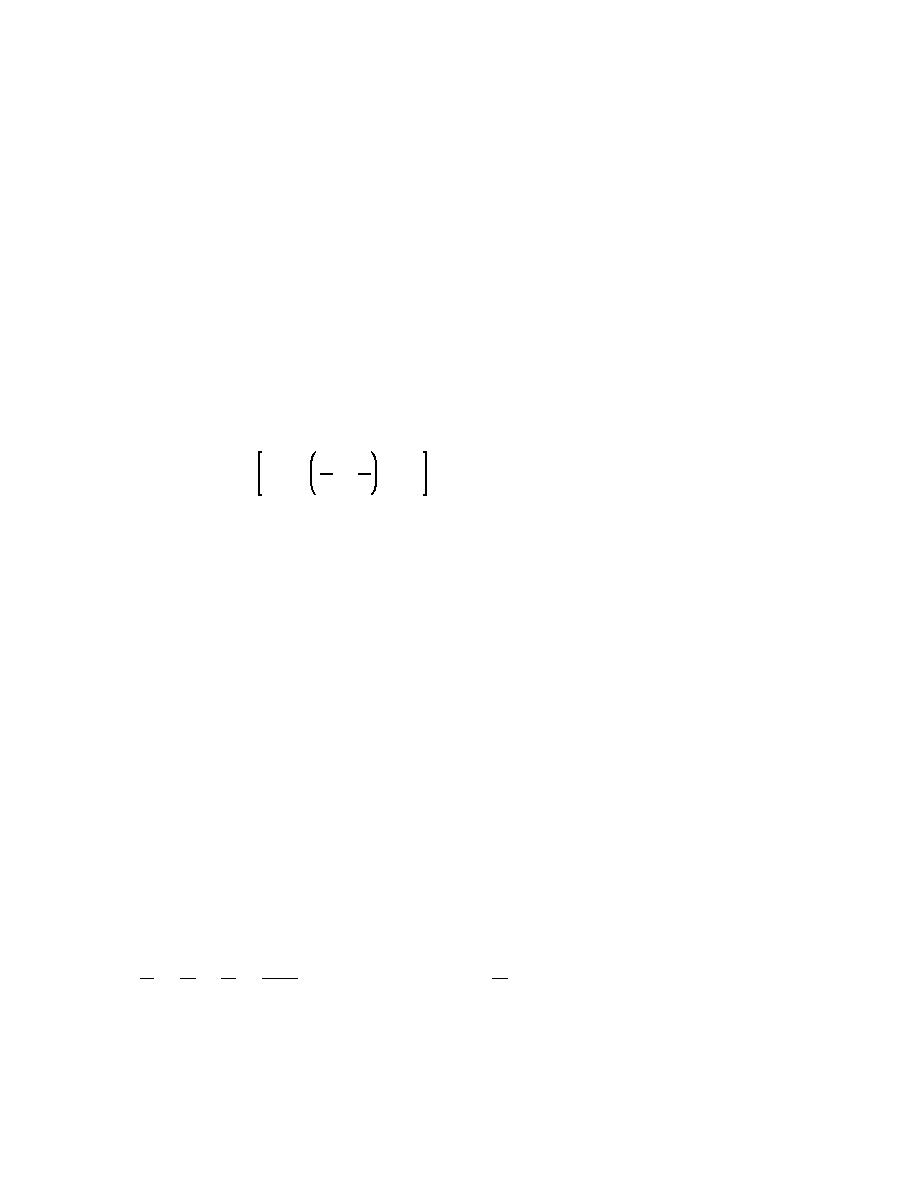
EM 1110-2-1100 (Part II)
30 Apr 02
series, Fenton (1979) developed a generalized recursion relationship for the KdV solution of any order.
Fenton's fifth- and ninth-order approximations are frequently used in practice. A summary of formulas of
the cnoidal wave theory are provided below. See Fenton (1979), Fenton and McKee 1990), and Miles (1981)
for a more comprehensive theoretical presentation.
(e) Long, finite-amplitude waves of permanent form propagating in shallow water may be described by
cnoidal wave theory. The existence in shallow water of such long waves of permanent form may have first
been recognized by Boussinesq (1871). However, the theory was originally developed by Korteweg and de
Vries (1895).
(f) Because local particle velocities, local particle accelerations, wave energy, and wave power for
cnoidal waves are difficult to describe such descriptions are not included here, but can be obtained in
graphical form from Wiegel (1960, 1964). Wave characteristics are described in parametric form in terms
of the modules k of the elliptic integrals. While k itself has no physical significance, it is used to express the
relationships between various wave parameters. Tabular presentations of the elliptic integrals and other
important functions can be obtained from the above references. The ordinate of the water surface ys measured
above the bottom is given by
x
t
ys ' yt % H cn 2 2 K (k)
, k
(II-1-77)
&
L
T
where
yt = distance from the bottom to the wave trough
H = trough to crest wave height
cn = elliptic cosine function
K(k) = complete elliptic integral of the first kind
k = modulus of the elliptic integrals
(g) The argument of cn2 is frequently denoted simply by ( ); thus, Equation II-1-77 above can be written
as
ys ' yt % H cn 2( )
(II-1-78)
(h) The elliptic cosine is a periodic function where cn2 [2K(k) ((x/L) - (t/T)] has a maximum amplitude
equal to unity. The modulus k is defined over the range 0 and 1. When k = 0, the wave profile becomes a
sinusoid, as in the linear theory; when k = 1, the wave profile becomes that of a solitary wave.
(i) The distance from the bottom to the wave trough yt, as used in Equations II-1-77 and II-1-78, is given
by
yt
yc
16d 2
H
H
K(k) [K(k) & E(k)] % 1 &
(II-1-79)
'
&
'
d
d
d
d
2
3L
where yc is the distance from the bottom to the crest, and E(k) the complete elliptic integral of the second kind.
Wavelength is given by
II-1-38
Water Wave Mechanics



 Previous Page
Previous Page
