Maximum wave steepness.

EM 1110-2-1100 (Part II)

30 Apr 02

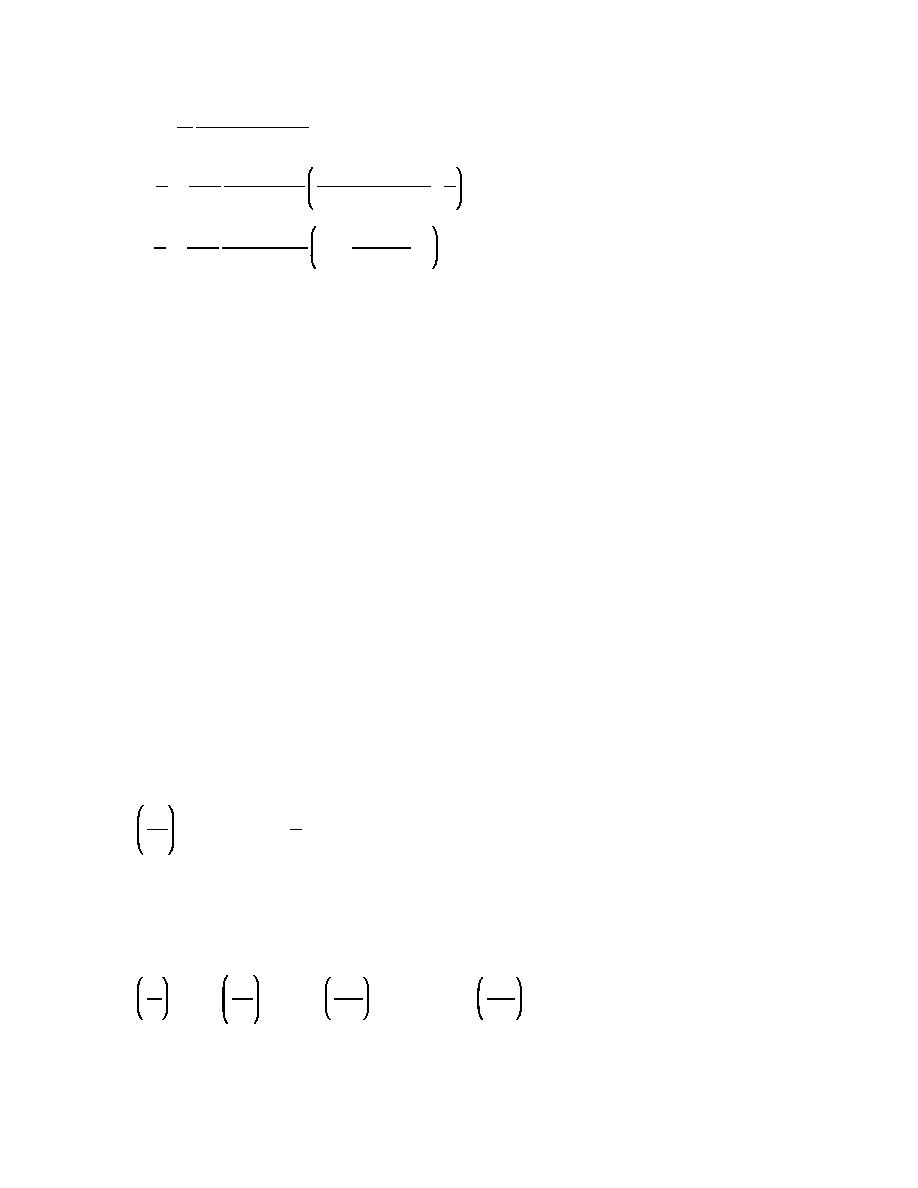
H cosh[2π(z % d)/L]

cos θ & ρgz

p ' ρg

2 cosh(2πd/L)

(II-1-70)

3 πH 2 tanh(2πd/L] cosh[4π(z % d)/L] 1

% ρg

& cos 2θ

L sinh2(2πd/L

8

3

2

sinh (2πd/L)

πH 2 tanh(2πd/L)

1

4π(z % d)

ρg

&1

cosh

&

L sinh (2πd/L)

8

L

2

(b) The terms proportional to the wave height squared in the above equation represent corrections by the

second-order theory to the pressure from the linear wave theory. The third term is the steady component of

pressure that corresponds to time-independent terms mentioned earlier.

(c) A direct byproduct of the high-order Stokes expansion is that it provides means for comparing

different orders of resulting theories, all of which are approximations. Such comparison is useful to obtain

insight about the choice of a theory for a particular problem. Nonetheless, it should be kept in mind that

linear (or first-order) theory applies to a wave that is symmetrical about the SWL and has water particles that

move in closed orbits. On the other hand, Stokes' higher-order theories predict a wave form that is

asymmetrical about the SWL but still symmetrical about a vertical line through the crest and has water

particle orbits that are open (Figure II-1-10).

(4) Maximum wave steepness.

(a) A progressive gravity wave is physically limited in height by depth and wavelength. The upper limit

or breaking wave height in deep water is a function of the wavelength and, in shallow and transitional water,

is a function of both depth and wavelength.

(b) Stokes (1880) predicted theoretically that a wave would remain stable only if the water particle

velocity at the crest was less than the wave celerity or phase velocity. If the wave height were to become so

large that the water particle velocity at the crest exceeded the wave celerity, the wave would become unstable

and break. Stokes found that a wave having a crest angle less than 120 deg would break (angle between two

lines tangent to the surface profile at the wave crest). The possibility of the existence of a wave having a crest

angle equal to 120 deg is known (Lamb 1945). Michell (1893) found that in deep water the theoretical limit

for wave steepness is

H0

1

' 0.142 .

(II-1-71)

L0

7

max

Havelock (1918) confirmed Michell's finding.

(c) Miche (1944) gives the limiting steepness for waves traveling in depths less than L0/2 without a

change in form as

H0

H

2πd

tanh

(II-1-72)

' 0.142 tanh

'

L0

L

max

Water Wave Mechanics

II-1-35