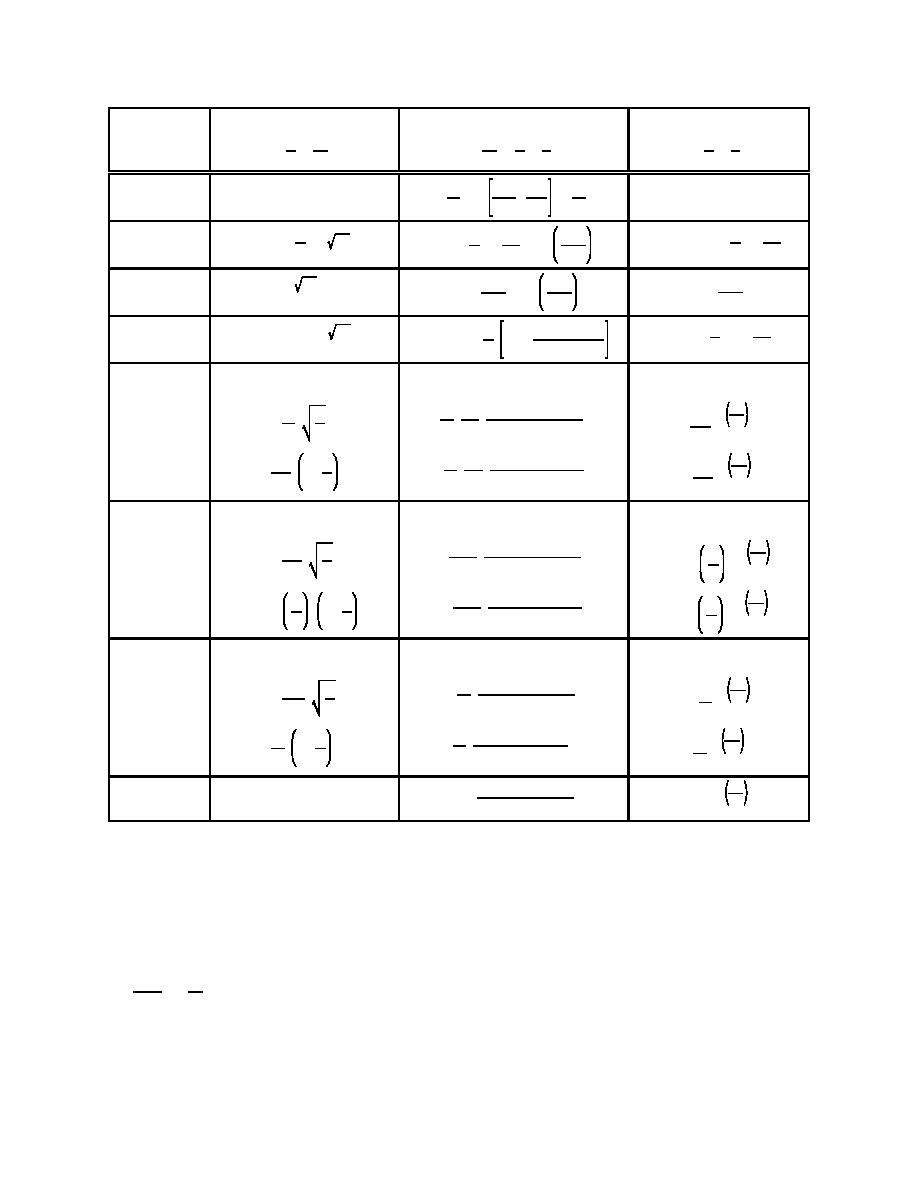
EM 1110-2-1100 (Part II)
30 Apr 02
Relative Depth
Shallow Water
Transitional Water
Deep Water
d
1
1
d
1
d
1
<
<
<
<
L
25
25
L
2
L
2
< Same As
1. Wave profile
Same As >
H
2πx 2πt
H
cos
cos θ
η'
&
'
2
L
T
2
L
L
gT
2. Wave celerity
L
gT
2πd
C ' C0 '
C'
' gd
'
tanh
C'
'
T
T
2π
T
2π
L
3. Wavelength
gT 2
gT 2
2πd
L ' T gd ' C T
L ' L0 '
' C0 T
tanh
L'
2π
L
2π
1
gT
4. Group velocity
1
4πd/L
Cg ' C ' gd
C'
Cg '
C
Cg ' n C '
1%
2
4π
2
sinh (4πd/L)
5. Water particle
velocity
H gT cosh [2π(z%d)/L]
(a) Horizontal
2πz
H
g
πH
u'
cos θ
cos θ
u'
L
e
u'
cos θ
2 L
cosh (2πd/L)
2
d
T
H gT sinh [2π(z%d)/L]
(b) Vertical
2πz
Hπ
z
πH
sin θ
w'
sin θ
w'
1%
L
e
w'
sin θ
2 L
cosh (2πd/L)
T
d
T
6. Water particle
gπH cosh [2π(z%d)/L]
(a) Horizontal
2πz
Hπ
g
2
π
ax '
sin θ
sin θ
ax '
L
ax ' 2 H
e
sin θ
L
cosh (2πd/L)
T
d
T
gπH sinh [2π(z%d)/L]
(b) Vertical
2
2πz
π
z
2
π
az ' &
cos θ
cos θ
az ' &2 H
1%
L
az ' &2 H
e
cos θ
L
cosh (2πd/L)
T
d
T
7. Water particle
displacements
H cosh [2π(z%d)/L]
(a) Horizontal
2πz
HT
g
H
ξ'&
sin θ
sin θ
ξ'&
L
ξ'& e
sin θ
2
sinh (2πd/L)
4π
d
2
H sinh [2π(z%d)/L]
(b) Vertical
2πz
H
z
H
cos θ
ζ'
cos θ
ζ'
1%
L
e
ζ'
cos θ
2
sinh (2πd/L)
2
d
2
p ' ρ g (η&z)
cosh [2π(z%d)/L]
8. Subsurface
2πz
&ρgz
p ' ρgη
L
pressure
p ' ρgη e
&ρgz
cosh (2πd/L)
Figure II-1-9. Summary of linear (Airy) wave theory - wave characteristics
assumption may be questionable. A third dimensionless parameter, which may be used to replace either the
wave steepness or relative water depth, may be defined as the ratio of wave steepness to relative water depth.
Thus,
H/L
H
(II-1-66)
'
d/L
d
Water Wave Mechanics
II-1-31



 Previous Page
Previous Page
