EM 1110-2-1100 (Part II)
30 Apr 02
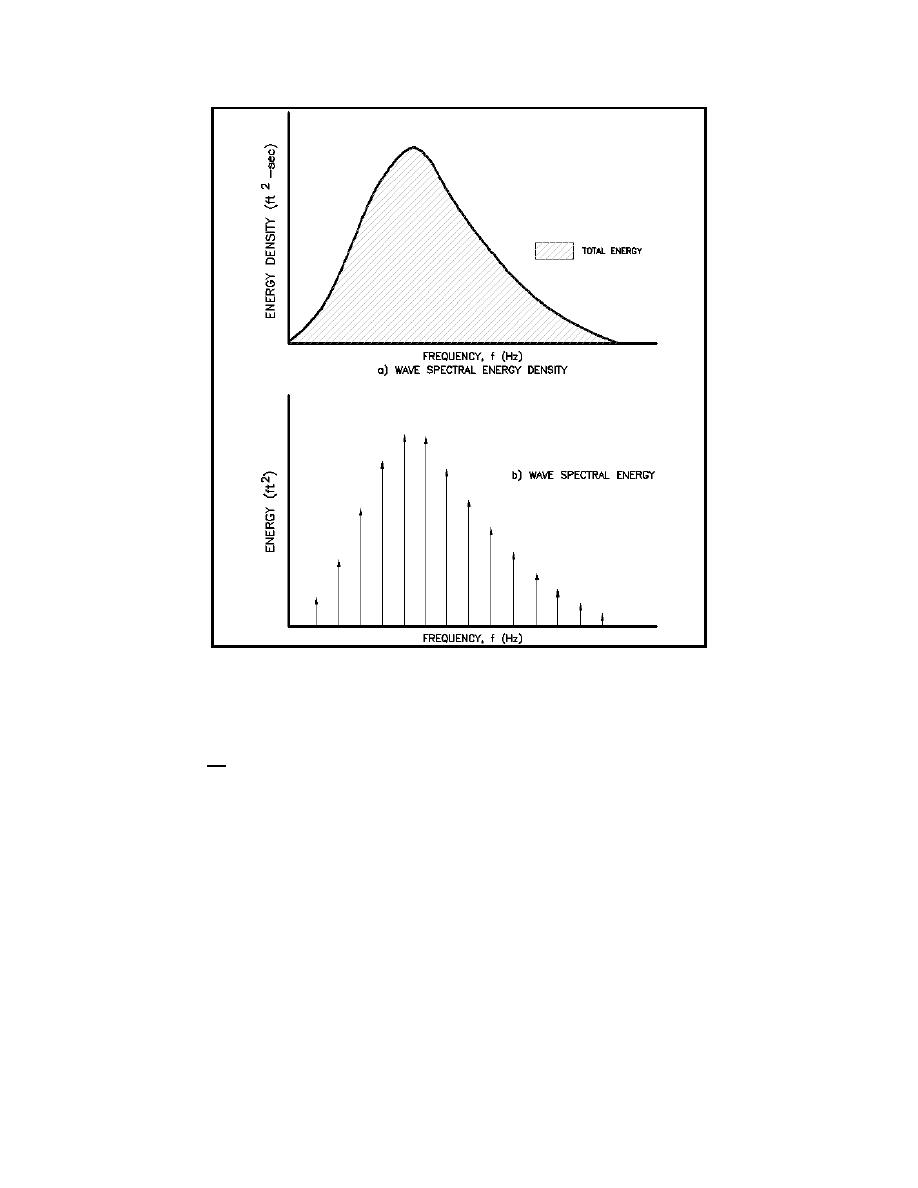
Figure II-1-35. Sketches of wave spectral energy and energy density
(Chakrabarti 1987)
2
4
'j
4
an
m
2
ση
E(f) df ' m0
(II-1-147)
'
2
n'1
0
where m0 is the zero-th moment of the spectrum. Physically, m0 represents the area under the curve of E(f).
The area under the spectral density represents the variance of a random signal whether the one-sided or two-
sided spectrum is used.
(l)
The moments of a spectrum can be obtained by
4
m
f i E(t) df
i ' 0,1,2,...
mi '
(II-1-148)
0
(m) We now use the above definition of the variance of a random signal to provide a third definition of
the significant wave height. As stated earlier, this gives an estimate of the significant wave height by the
wave spectrum. For Rayleigh distributed wave heights, Hs may be approximated (Longuet-Higgins 1952)
by
II-1-84
Water Wave Mechanics



 Previous Page
Previous Page
