EM 1110-2-1100 (Part II)
30 Apr 02
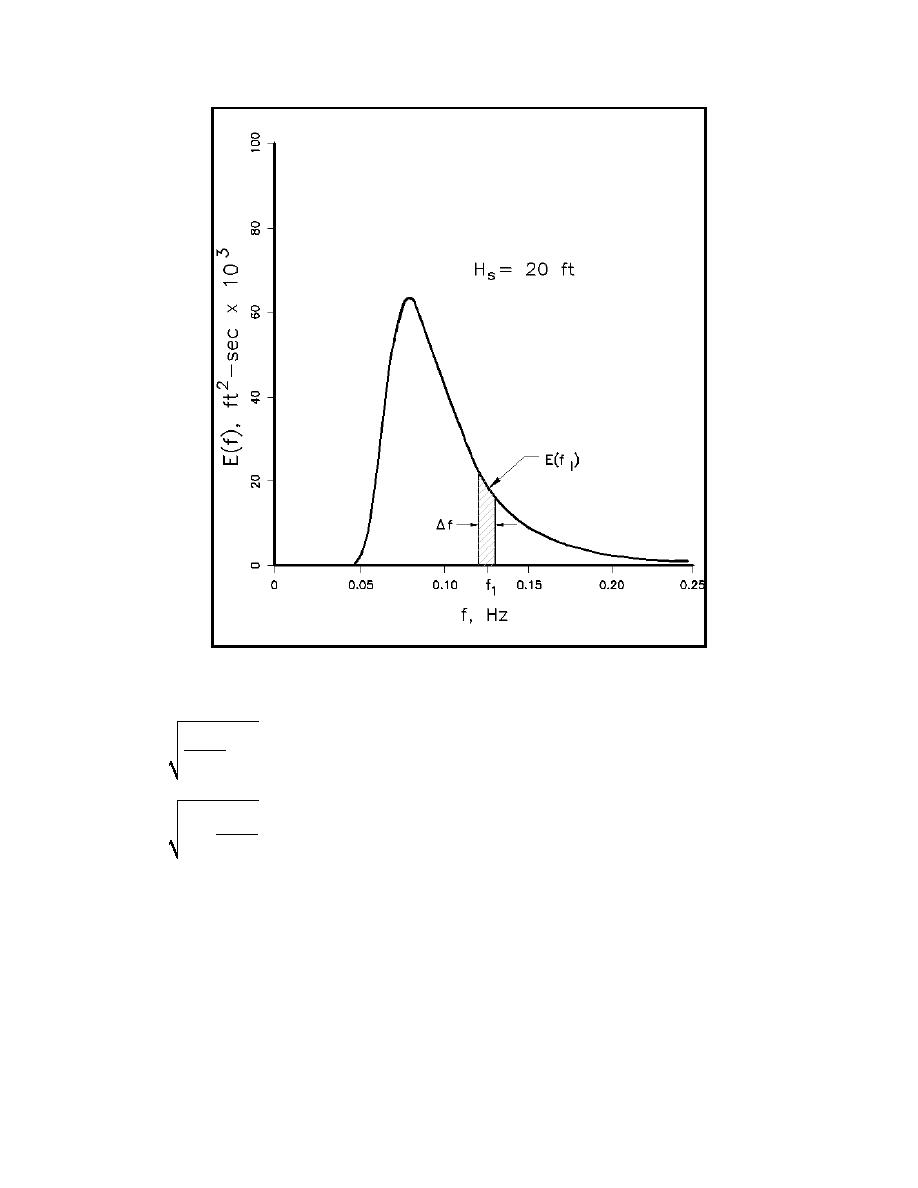
Figure II-1-37. Energy density and frequency relationship (Chakrabarti 1987)
m0 m2
&1
ν'
2
m1
(II-1-150)
2
m2
ε'
1&
m0 m4
(b) For a narrow-band spectrum, both ν and ε must be close to 0 (Figure II-1-38). For example, for the
two most common empirical spectra, the Pierson-Moskowitz (PM) spectrum (Pierson and Moskowitz 1964)
and the JONSWAP spectrum (Hasselmann et al. 1973), which are discussed in the next section, ν = 0.425 and
0.389, respectively, with ε = 1 for both. Natural ocean waves, therefore, have a broad-banded spectrum.
(c) The values of ε obtained from a wave energy spectrum are generally not considered as the sole
indication of how broad the spectra are. This is due to the amplification of the noise present in the wave
energy spectral density at higher frequencies that enters into the calculation of the higher moments m2 and
m4 in the above equation for ε. Goda (1974) proposed a spectral peakedness parameter called Qp defined as
II-1-86
Water Wave Mechanics



 Previous Page
Previous Page
