EM 1110-2-1100 (Part II)
30 Apr 02
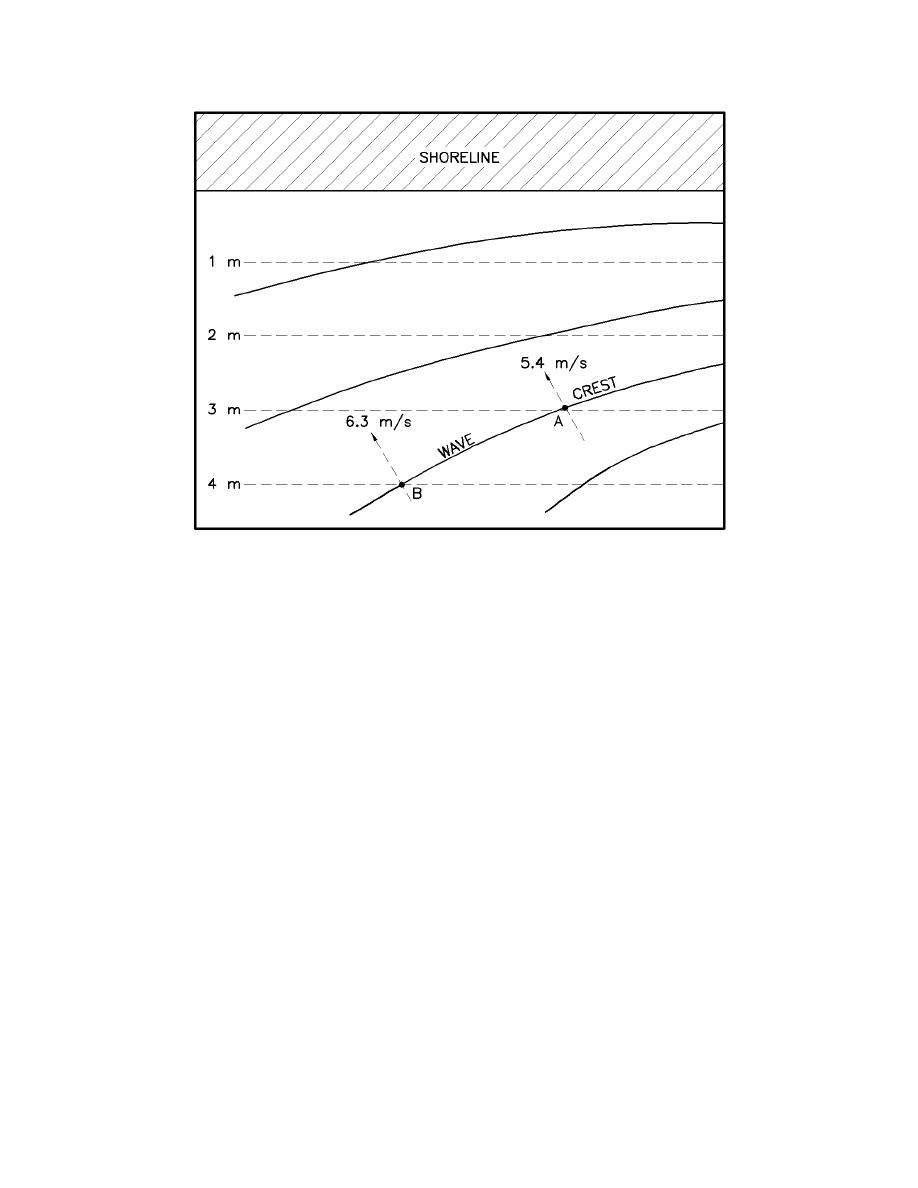
Figure II-3-3. Straight shore with all depth contours evenly spaced and parallel to
the shoreline
have been superseded by the numerical methods discussed in Part II, Section 3-5. Refraction and shoaling
analyses typically try to specify the wave height and direction along a ray.
(2) Figure II-3-4 provides idealized plots of wave rays for several typical types of bathymetry. Simple
parallel contours tend to reduce the energy of waves inshore if they approach at an angle. Shoals tend to
focus rays onto the shoals and spread energy out to either side. Canyons tend to focus energy to either side
and reduce energy over the head of the canyon. The amount of reduction or amplification will depend not
only on bathymetry, but on the initial angle of approach and period of the waves. For natural sea states that
have energy spread over a range of frequencies and directions, reduction and amplification are also dependent
upon the directional spread of energy (Vincent and Briggs 1989).
(3) Refraction and shoaling have been derived and treated widely. The following presentation follows
that of Dean and Dalrymple (1991) very closely. Other explanations are provided in Ippen (1966), the Shore
Protection Manual (1984), and Herbich (1990).
b. Straight and parallel contours.
(1) First, the equation for specifying how wave angle changes along the ray is developed, followed by
the equation for wave height. The derivation is only for parallel and straight contours with no currents
present. The x-component of the coordinate system will be taken to be orthogonal to the shoreline; the y-
coordinate is taken to be shore-parallel. The straight and shore-parallel contours assumption will imply that
any derivative in the y-direction is zero because dh/dy is zero.
Estimation of Nearshore Waves
II-3-7



 Previous Page
Previous Page
