EM 1110-2-1100 (Part II)
31 July 2003
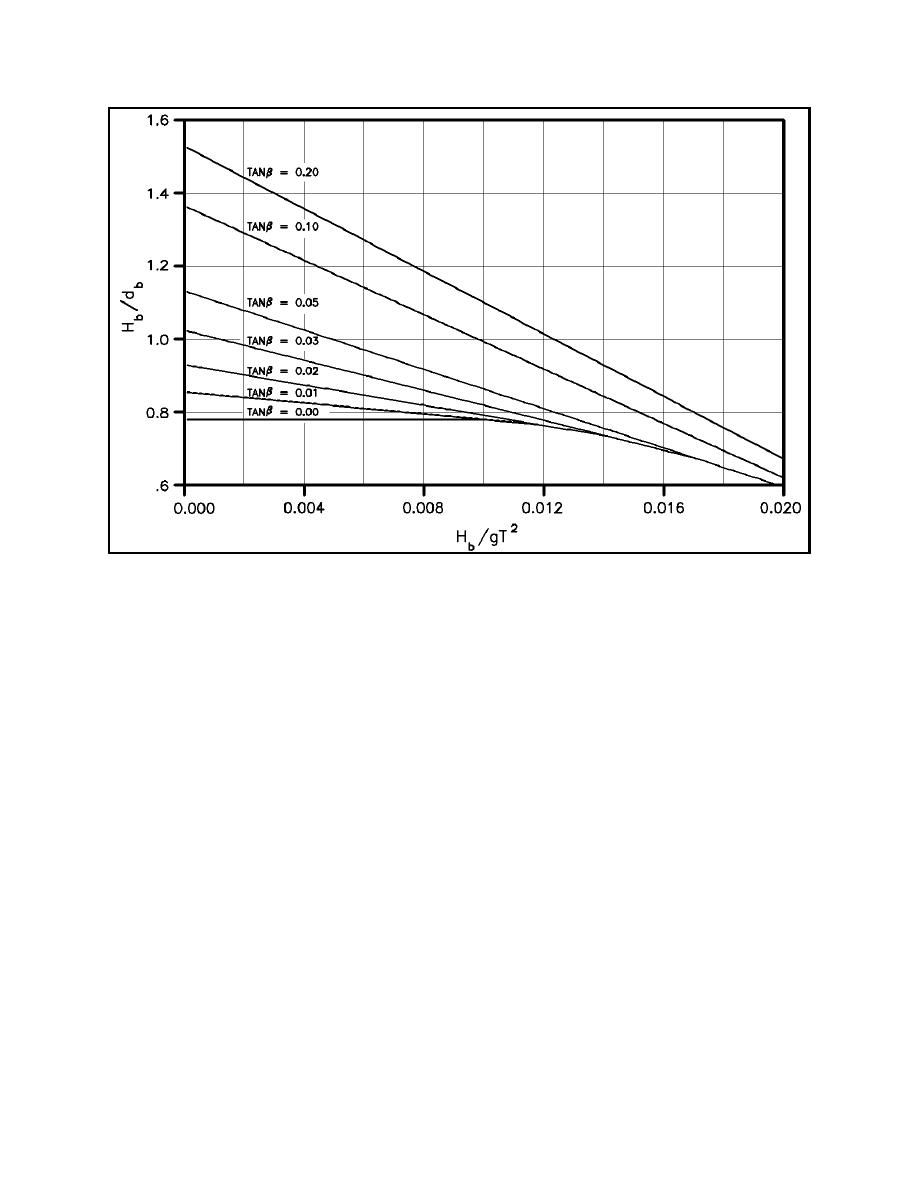
Breaker depth index as a function of Hb/(gT2) (Weggel 1972)
Figure II-4-2.
b. Wave transformation in the surf zone. Following incipient wave breaking, the wave shape changes
rapidly to resemble a bore (Svendsen 1984). The wave profile becomes sawtooth in shape with the leading
edge of the wave crest becoming nearly vertical (Figure II-4-3). The wave may continue to dissipate energy
to the shoreline or, if the water depth again increases as in the case of a barred beach profile, the wave may
cease breaking, re-form, and break again on the shore. The transformation of wave height through the surf
zone impacts wave setup, runup, nearshore currents, and sediment transport.
(1) Similarity method. The simplest method for predicting wave height through the surf zone, an
extension of Equation II-4-3 shoreward of incipient breaking conditions, is to assume a constant height-to-
depth ratio from the break point to shore
Hb ' γb db
(II-4-12)
This method, also referred to as saturated breaking, has been used successfully by Longuet-Higgins and
Stewart (1963) to calculate setup, and by Bowen (1969a), Longuet-Higgins (1970a,b), and Thornton (1970)
to calculate longshore currents. The similarity method is applicable only for monotonically decreasing water
depth through the surf zone and gives best results for a beach slope of approximately 1/30. On steeper slopes,
Equation II-4-12 tends to underestimate the wave height. On gentler slopes or barred topography, it tends
to overestimate the wave height. Equation II-4-12 is based on the assumption that wave height is zero at the
mean shoreline (see Part II-4-3 for discussion of mean versus still-water shoreline). Camfield (1991) shows
that a conservative estimate of wave height at the still-water shoreline is 0.20 Hb for 0.01 # tan β # 0.1.
Surf Zone Hydrodynamics
II-4-5



 Previous Page
Previous Page
