EM 1110-2-1100 (Part II)
31 July 2003
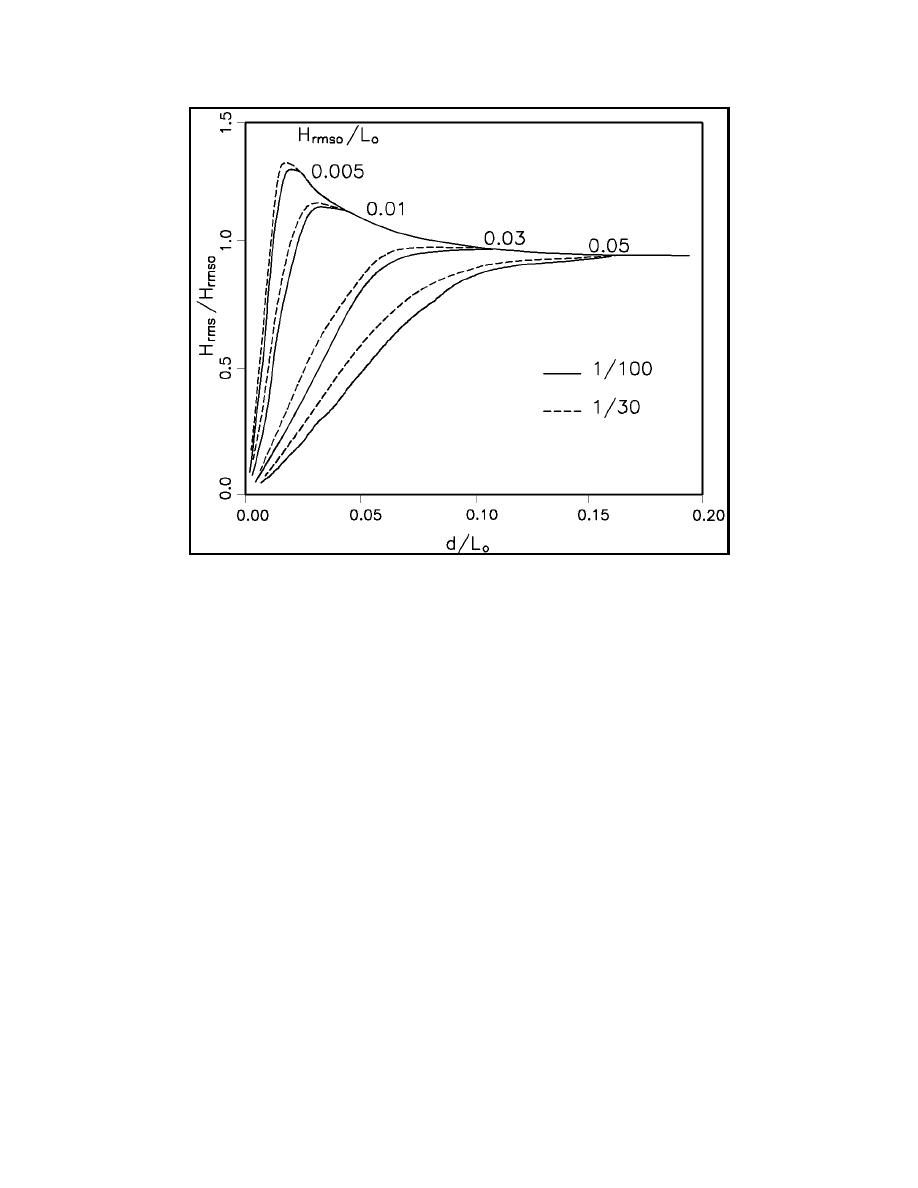
Figure II-4-4. Transformation of Hrms with depth based on the individual wave
approach and the Dally, Dean, and Dalrymple (1985) model
and Dalrymple (1985) wave decay model (monochromatic or irregular waves). The main assumption
underlying the model is uniformity of waves and bathymetry alongshore, but the beach profile can be
irregular across the shore (e.g., longshore bars and nonuniform slopes). NMLONG uses a single wave period
and direction and applies a Rayleigh distribution wave heights outside the surf zone. The model runs on a
personal computer and has a convenient graphical interface. NMLONG calculates both wave transformation
and longshore current (which will be discussed in a later section) for arbitrary offshore (input) wave
conditions and provides a plot of results. Figure II-4-5 gives an example NMLONG calculation and a
comparison of wave breaking field measurements reported by Thornton and Guza (1986).
(d) A second statistical approach is based on assuming a wave height distribution in the surf zone. The
Rayleigh distribution is a reliable measure of the wave height distribution in deep water and at finite depths.
In the surf zone, depth-induced breaking acts to limit the highest waves in the distribution, contrary to the
Rayleigh distribution, which is unbounded. The surf zone wave height distribution has generally been
represented as a truncated Rayleigh distribution (e.g., Collins (1970), Battjes (1972), Kuo and Kuo (1974),
Goda 1975). Battjes and Janssen (1978) and Thornton and Guza (1983) base the distribution of wave heights
at any point in the surf zone on a Rayleigh distribution or a truncated Rayleigh distribution (truncated above
a maximum wave height for the given water depth). A percentage of waves in the distribution is designated
as broken, and energy dissipation from these broken waves is calculated from Equation II-4-13 through a
model of dissipation similar to a periodic bore. Battjes and Janssen (1978) define the energy dissipation as
δ = 0.25 ρ gQb f m ( H max ) 2
(II-4-17)
Surf Zone Hydrodynamics
II-4-9



 Previous Page
Previous Page
