EM 1110-2-1100 (Part II)
30 Apr 02
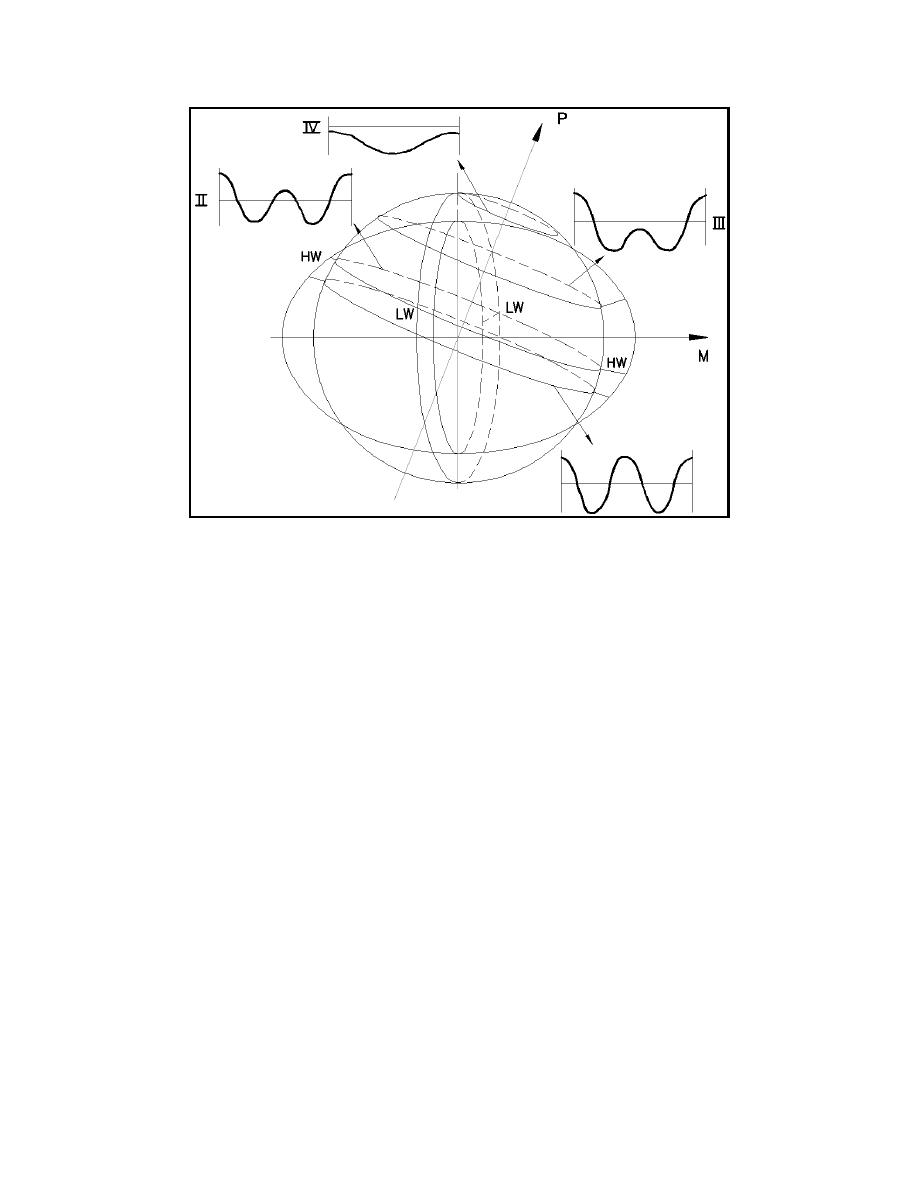
Figure II-5-7.
The daily inequality (Dronkers 1964)
and the entrance to the Savannah River at Savannah, GA, are shown in the figure. Each time series exhibits
two distinct and nearly equal tides per day. As one moves to Key West, FL, the character of the tide begins
to change with a noticeable diurnal inequality. Tides inside the Gulf of Mexico range from semidiurnal at
Key West, FL, to diurnal at Pensacola, FL, to mixed at Galveston, TX. Note that the Galveston data
progresses from a diurnal tide during the first third of the record to a semidiurnal tide. Tides in the Gulf of
Mexico are more complex than open ocean stations because astronomical forcing is modified by
geometrically forced nodes and antinodes. These seiche-related phenomena are discussed in Part II-5-6.
Pacific coast tides, shown in Figure II-5-9, are generally of larger amplitude than Atlantic and Gulf coast tides
and often have a decided diurnal inequality.
b. Tidal time series analysis.
(1) Introduction. The equilibrium theory of tides is a hypothesis that the waters of the earth respond
instantaneously to the tide-producing forces of the sun and moon. For example, high water occurs directly
beneath the moon and sun, i.e., at the sublunar and subsolar points. This tide is referred to as an equilibrium
tide. Part II-5-3 a (1), states that tide-producing forces are written in a polynomial expansion approximation
for the exact solution of Equations II-5-12 and II-5-13. These expansion terms involve astronomical
arguments describing the location of the sun and moon as well as the location of the observer on the earth.
Although several variational forms of the series expansion have been published, the development presented
in Schureman (1924) is given below. Alternate forms of expansion are discussed in Dronkers (1964).
(2) Harmonic constituents.
(a) According to equilibrium theory, the theoretical tide can be predicted at any location on the earth as
a sum of a number of harmonic terms contained in the polynomial expansion representation of the
Water Levels and Long Waves
II-5-11



 Previous Page
Previous Page
