EM 1110-2-1100 (Part II)
30 Apr 02
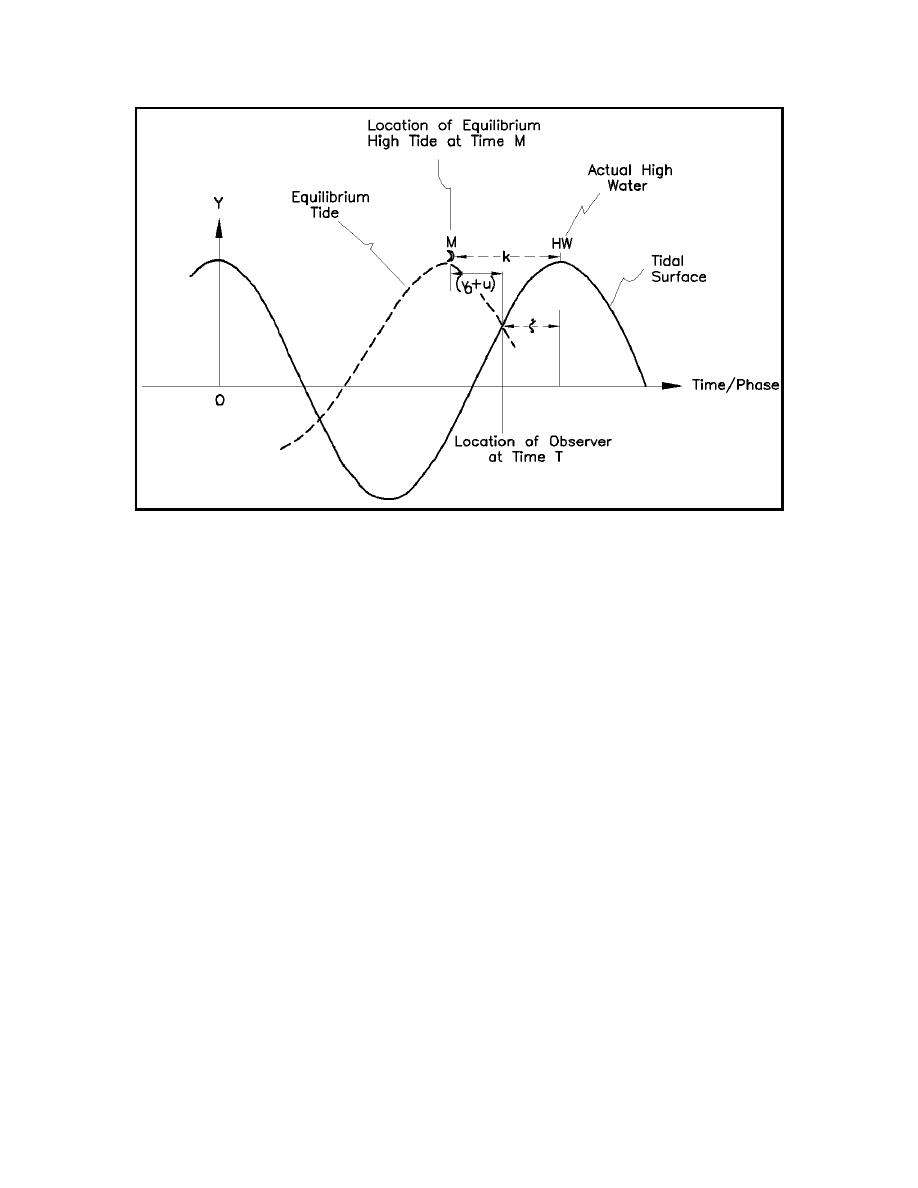
Figure II-5-10.
Tidal phase relationships
(m) A tidal simulation computer program is available in ACES (Leenknecht, Szuwalski, and Sherlock
1992) to compute nodal factors and local (or Greenwich) equilibrium argument values for any time period
and generate the corresponding water surface time series as a function of input constituent amplitudes.
Formulas for computing the equilibrium arguments are found in Shureman (1924), but are too lengthy for this
manual.
(3) Harmonic reconstruction.
(a) In order to reconstruct a tidal series for a specific time and location, the various phase arguments
of Equation II-5-16 must be defined according to local conditions. Generally, local values of κn, H0, and Hn
are available from NOS harmonic analyses. Because the values of the nodal factors fn are slowly varying,
the yearly values determined according to Schureman are sufficiently accurate for the particular time of
interest throughout the world. However, local values of (V0 + u)n vary with the speed of the constituent and
have to be determined for the location and time of interest. This information can be computed from tabulated
equilibrium arguments relative to Greenwich such as those presented in Schureman or computed with
programs developed for that purpose such as those contained in ACES.
(b) Values of the local equilibrium arguments, i.e., local (V0 + u)n, represent the instantaneous value of
each of the equilibrium tide-producing force constituents (in degrees) with respect to some specific point on
the earth; for example, the time-varying location of the moon and sun with respect to some location on the
earth. Referring to Figure II-5-11, the horizontal axis represents distance with the point G representing
Greenwich, England, and O representing an observer located at some point west of Greenwich. The location
of the moon with respect to Greenwich at longitude 0o at Greenwich time t0 is indicated by the Greenwich
equilibrium argument presented in Shureman, denoted as Greenwich (V0 + u), for time Greenwich t0.
II-5-18
Water Levels and Long Waves



 Previous Page
Previous Page
