EM 1110-2-1100 (Part II)
30 Apr 02
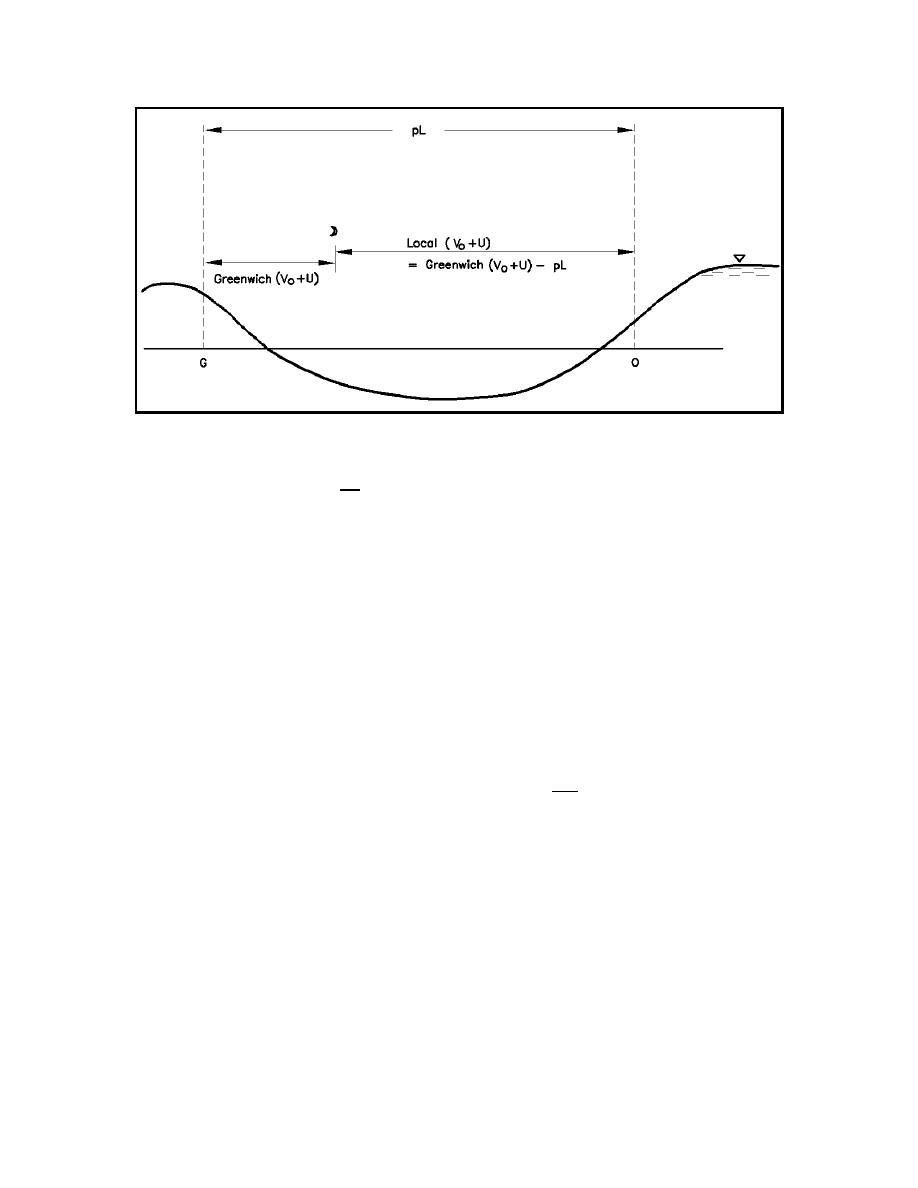
Figure II-5-11.
Phase angle argument relationship
S
Greenwich (t0) ' local (t0) %
(II-5-17)
15
where S is the local time meridian (shown on NOS analyses) and the number 15 indicates a time change of
1 hr per 15 deg longitude.
(e) The speed of the time argument (ant in Equation II-5-16) in degrees with respect to time is equal to
the speed of the constituent an multiplied by Equation II-5-17. Therefore, the final relationship between local
and Greenwich phase arguments that account for both differences in location (-pL) and local time (aS/15) can
be written as:
local (V0 % u) ' Greenwich (V0 % u) & pL
(II-5-18)
Therefore, a tide at any arbitrary location is computed as
H(t)local ' H0 % j fnHncos [ant % Greenwich V0 % u) & pL %
N
anS
& κn]
(II-5-19)
15
n'1
(f) A reconstructed tidal time series of a published NOS harmonic analysis is presented for Sandy Hook,
NJ. The NOS analysis is shown in Figure II-5-12. As can be seen by the reported amplitudes, the M2, S2, N2,
K1, Sa, O1, ν2, and K2 constituents contain the majority of the tidal energy. These constituents are used to
generate a 15-day tidal signal beginning on 1 January 1984 at 0000 hr Eastern Standard Time. Computed
values are compared to the high and low tide predictions published in the Tide Tables for 1984 (NOAA 1984)
shown in Figure II-5-13. Because all 37 constituents are not used in the reconstruction, the match is not
perfect; however, it demonstrates the degree of accuracy that can be achieved by using only major
constituents.
II-5-20
Water Levels and Long Waves



 Previous Page
Previous Page
