EM 1110-2-1100 (Part II)
30 Apr 02
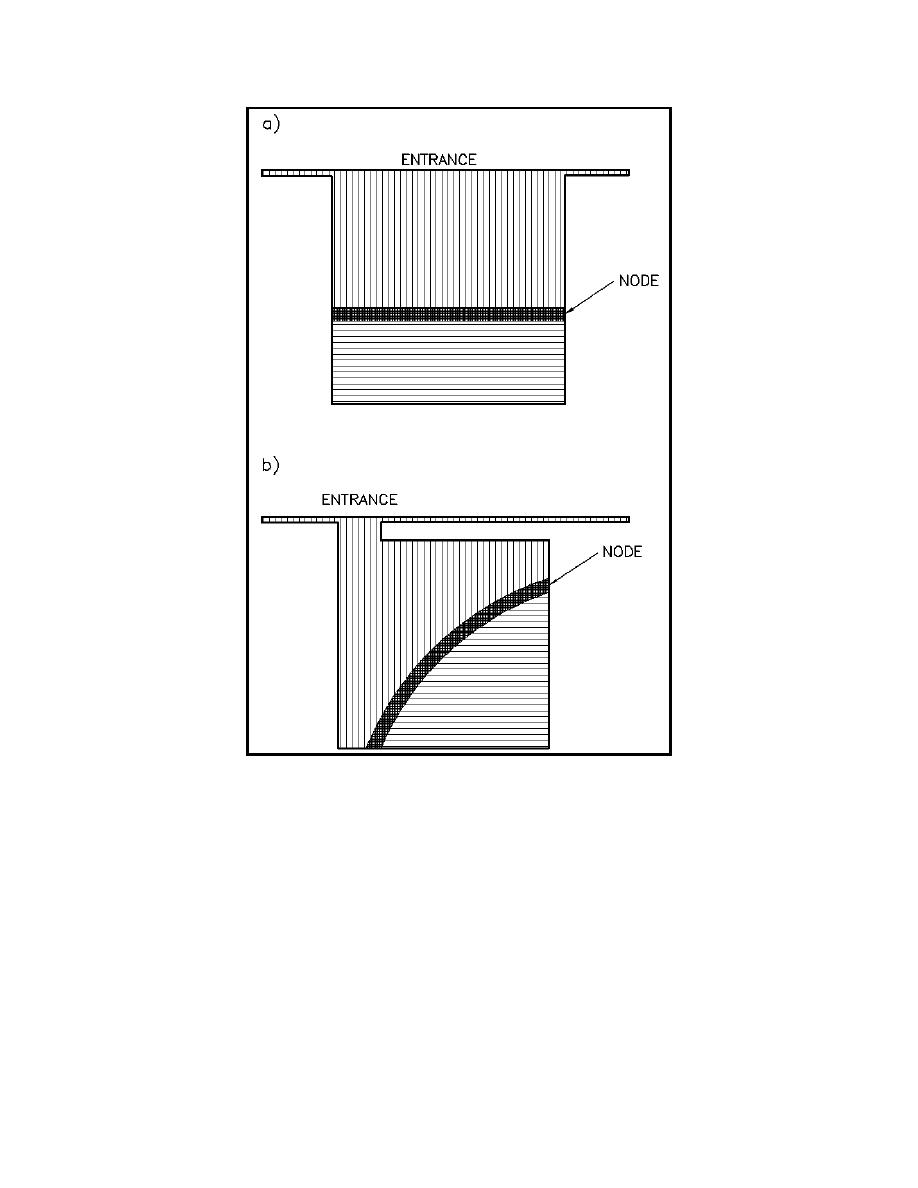
Figure II-7-32. Node locations for a dominant mode of oscillation
in a square harbor: a) fully open; b) asymmetric, constricted
entrance
physical modeling for periods longer than 400 sec. Both modeling tools can be used effectively for the
shorter-period oscillations.
(4) Numerical models can reproduce the geometry and bathymetry of a harbor area reasonably well and
estimate harbor response to long waves. Figure II-7-36 is an example numerical model grid. This grid is
finer than would normally be required for harbor oscillation studies because it was designed for both wind
waves and long waves. Numerical models can be used to generate harbor response curves as in Figure II-7-33
at various points in the harbor. Results for resonance conditions of particular interest can be displayed over
the whole harbor to show oscillation patterns. For example, amplification factors and phases calculated with
the example grid are presented for five wave periods, corresponding to resonant peaks in the main harbor
basin (Figures II-7-37 and II-7-38). Phases are relative to the incident wave. Phase plots are useful because
phases in a pure standing wave are constant up to a node and then change 180 deg across the
Harbor Hydrodynamics
II-7-41



 Previous Page
Previous Page
