EM 1110-2-1100 (Part II)
30 Apr 02
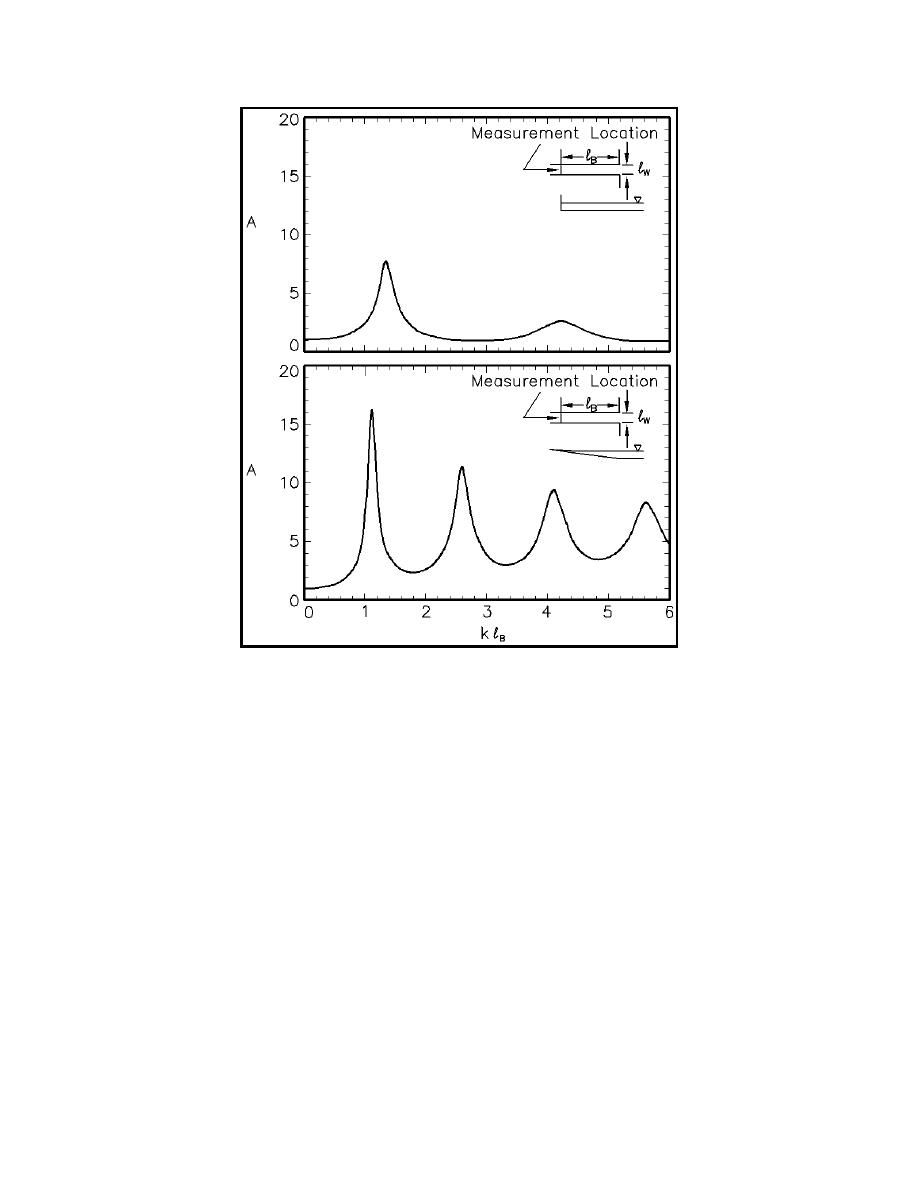
Figure II-7-33. Response curves for rectangular harbor with flat
and sloping bottom (Zelt 1986)
node. Thus, phase contour lines cluster together at node locations. Since regions of similar phase, plotted
with similar gray shades (or colors on a computer screen), move up and down together, the resonant modes
of oscillation can be much more easily visualized. This information about node locations and behavior of
resonant modes is quite useful in analyzing harbor oscillations.
(5) Limitations to numerical models relate to approximations in formulating the following items:
incident wave conditions, wave evolution during propagation over irregular bathymetry, wave interaction
with structures, and harbor boundary features. Numerical model technology is reviewed by Raichlen and Lee
(1992) and Abbott and Madsen (1990).
(6) The Corps of Engineers has traditionally used a steady-state, hybrid-element model based on the mild
slope equation (Chen 1986; Chen and Houston 1987; Cialone et al. 1991). Variable boundary reflection and
bottom friction are included. The seaward boundary is a semicircle outside the harbor entrance.
Monochromatic waves are incident along the semicircle boundary. Since the model is linear, results from
multiple monochromatic wave runs can be recombined to simulate a spectral response. The model does not
account for entrance losses (Thompson, Chen, and Hadley 1993).
II-7-42
Harbor Hydrodynamics



 Previous Page
Previous Page
