EM 1110-2-1100 (Part II)
30 Apr 02
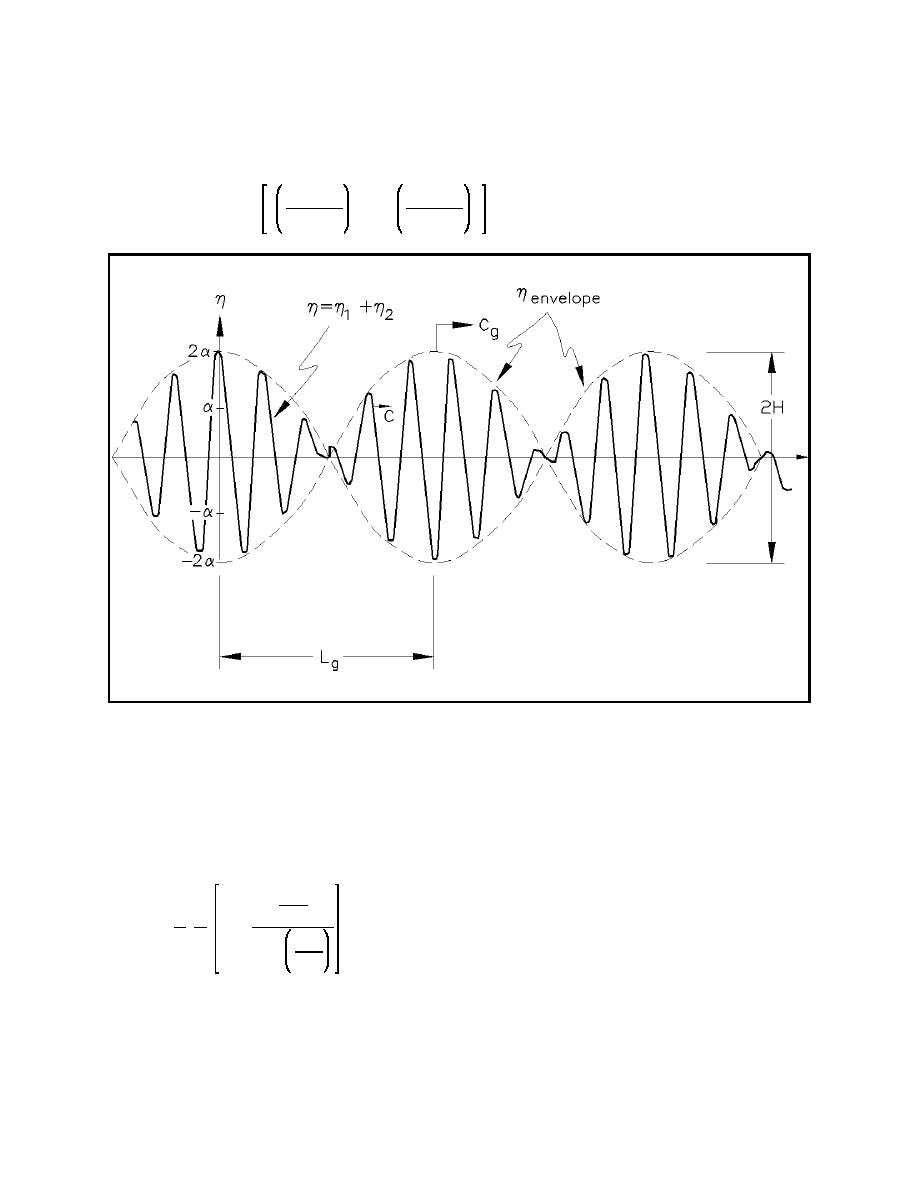
the resultant wave height will be zero. The surface profile made up of the sum of the two sinusoidal waves
is given by Equation II-1-47 and is shown in Figure II-1-6. The waves shown in Figure II-1-6 appear to be
traveling in groups described by the equation of the envelope curves
L2 & L1
T2 & T1
ηenvelope ' H cos π
x&π
t
(II-1-48)
L1 L2
T1 T2
Figure II-1-6. Characteristics of a wave group formed by the addition of sinusoids with different periods
(c) It is the speed of these groups (i.e., the velocity of propagation of the envelope curves) defined in
Equation II-1-48 that represents the group velocity. The limiting speed of the wave groups as they become
large (i.e., as the wavelength L1 approaches L2 and consequently the wave period T1 approaches T2) is the
group velocity and can be shown to be equal to
4πd
1 L
L
1%
' nC
Cg '
(II-1-49)
2 T
4πd
sinh
L
where
Water Wave Mechanics
II-1-25



 Previous Page
Previous Page
