EXAMPLE PROBLEM II-1-4

EM 1110-2-1100 (Part II)

30 Apr 02

FIND:

The height of the wave H assuming that linear theory applies and the average frequency corresponds to the

average wave amplitude.

GIVEN:

An average maximum pressure p = 124 kilonewtons per square meter is measured by a subsurface

pressure gauge located in salt water 0.6 meter (1.97 ft) above the bed in depth d = 12 m (39 ft). The average

frequency f = 0.06666 cycles per second (Hertz).

SOLUTION:

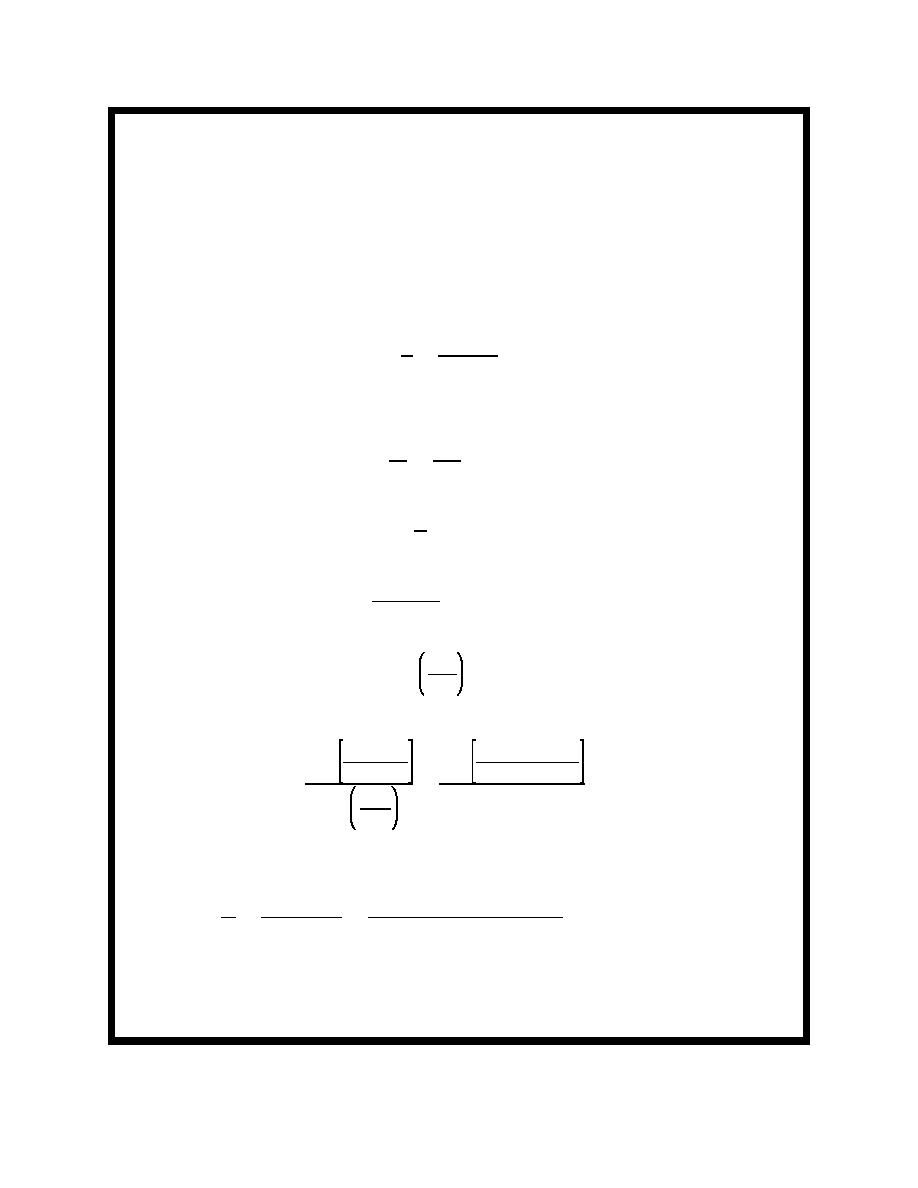
1

. 15 s

T'

'

f

(0.0666)

L0 ' 1.56T 2 ' 1.56(15)2 ' 351 m (1152 ft)

d

12

. 0.0342

'

L0

351

From Figure II-1-5, entering with d/L0,

d

' 0.07651

L

hence,

12

L'

' 156.8 m (515 ft)

(0.07651)

and

2πd

' 1.1178

cosh

L

Therefore, from Equation II-1-43

2 π (z % d)

2 π(&11.4 % 12)

cosh

L

156.8

Kz '

' 0.8949

'

1.1178

2πd

cosh

L

Since η = a = H/2 when the pressure is maximum (under the wave crest), and N = 1.0 since linear theory is

assumed valid,

H

N(p % ρgz)

1.0 [124 % (10.06) (&11.4)]

' 1.04 m (3.44 ft)

'

2

ρgKz

(10.06) (0.8949)

Therefore,

H ' 2(1.04) ' 2.08 m (6.3 ft)

Note that the value of K in Figure II-1-5 or SPM (1984) could not be used since the pressure was not measured

at the bottom.

II-1-24

Water Wave Mechanics