EM 1110-2-1100 (Part II)
30 Apr 02
EXAMPLE PROBLEM II-3-1
FIND:
Wave height H and angle θ at water depths of 200, 100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 16, 14, 12, 10, 8,
6, and 4 m for deepwater wave angles of 0o, 15o, and 45o.
GIVEN:
A wave 1 m high and 15-sec period in 500 m of water, with a plane, sloping beach.
SOLUTION:
Routine solutions for a plane beach can be obtained using the ACES wave transformation code, by direct
calculation, or graphically using Figure II-3-6.
Table II-3-1 provides the results obtained by directly using the ACES code. On a personal computer with a
486-level microprocessor, the results may be obtained in seconds.
For a wave with a depth of 10 m and an initial wave angle of 45 deg, wave height and angle are calculated as
follows:
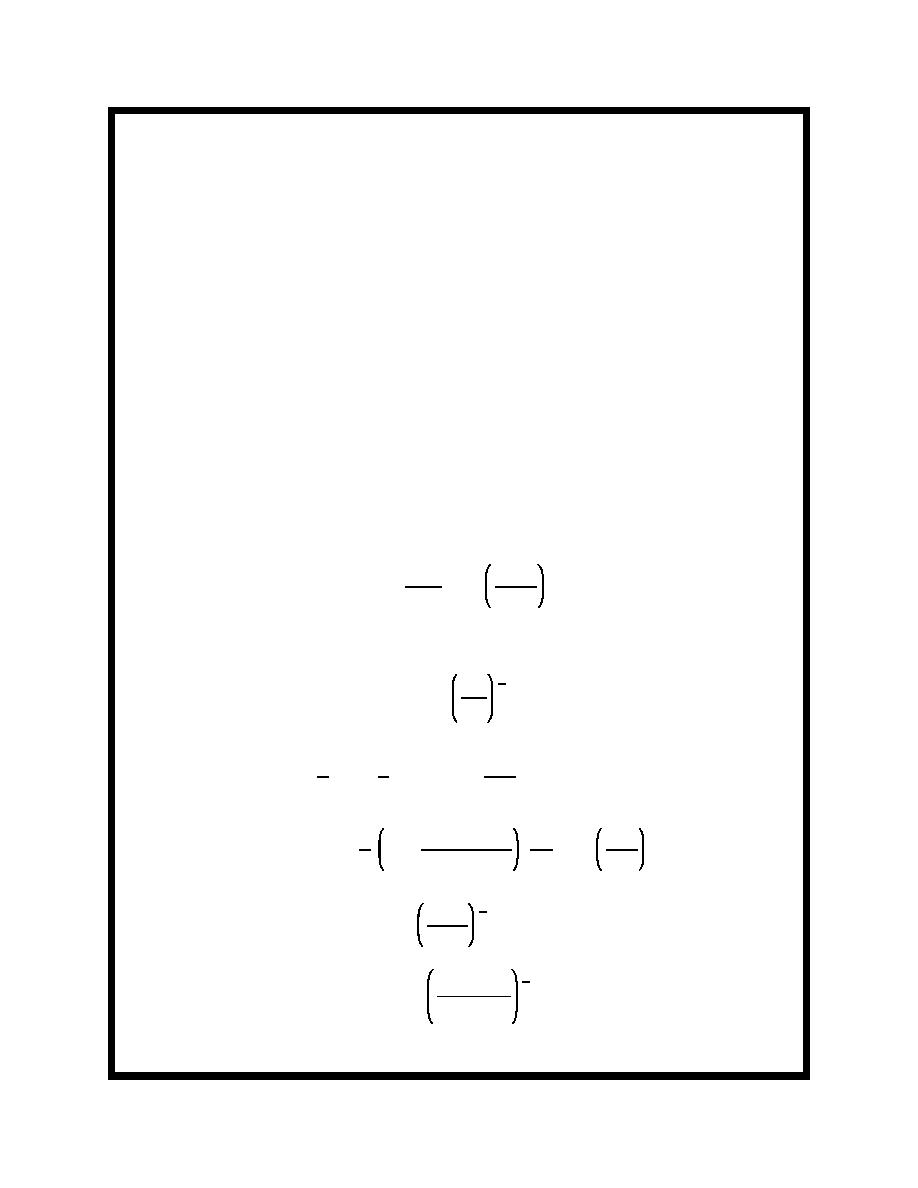
Since the deepwater wave length of a 15-sec wave is
L0 ' 1.56 T 2 ' 1.56 (15)2 ' 351 m
and since 500 m is greater than L0/2, the given initial wave is a deepwater condition. The wave length of the wave
in 10 m must be estimated from
g T2
2πd
L'
tanh
2π
L
and is 144 m (see Problem II-1-1).
The shoaling coefficient Ks can be estimated from
1
Cg0
2
Ks '
Cgl
In deep water Cg0 for a 15-sec wave is
1
1
23.4
C0 '
( 1.56 T ) '
' 11.7 m / s
2
2
2
The group velocity is given by
1
4 π d/L
gT
2πd
tanh
Cg ' n C '
1%
2
sinh (4 π d/L)
2π
L
Substitution of d = 10 m, L = 144 m, T = 15 sec, and g = 9.8 m/sec2 yields 9.05 m/s.
1
11.70
2
' 1.14
Ks '
9.05
Solution for Kr involves
1
1 & sin2θ0
4
Kr '
1 & sin2θ1
(Continued)
Estimation of Nearshore Waves
II-3-13



 Previous Page
Previous Page
