EM 1110-2-1100 (Part II)
30 Apr 02
(4) Other models. Other more sophisticated models that require considerable expertise to use already
exist or are being developed. The reader is advised to consult current technical literature for details.
Part II-5-7, "Numerical Modeling of Long Wave Hydrodynamics," discusses two such sophisticated models,
CH3D and ADCIRC.
(5) Physical models. Physical models have also been used for both the hydraulic and sedimentation
aspects of inlet studies, but numerical models usually have been used in recent years due to the expense of
constructing the large bay system of an inlet and the need to examine processes difficult to reproduce in a
physical model, such as storm surge, which would need to include wind effects. However, physical models
are appropriate and cost-effective for examining structures and detailed flow patterns in the immediate
vicinity of the inlet entrance (sample references include Bottin (1978, 1982), Seabergh (1975), Seabergh and
Lane (1977), and Seabergh and McCoy (1982)).
II-6-3. Hydrodynamic and Sediment Interaction at Tidal Inlets
a. Introduction. Waves, currents, and sediment interact at tidal inlets over a large physical area, with
varying effects over a tidal cycle (Smith 1991). At the throat or minimum cross-sectional area of the inlet
and bayward, tidal currents are the predominant forcing agent interacting with sediments. However, moving
seaward and alongshore away from the inlet, the effect of waves increases. Wave energy on the edges of the
inlet channel can contribute sediment from adjoining beaches, with the flood tidal currents tending to move
bayward to a flood tidal shoal (or middle-ground shoal), or the ebb currents jetting sediment seaward to settle
on the ebb shoal. Sediment may again be moved to adjoining beaches by the combination of waves and
currents, thus "bypassing" the inlet. The interaction of tidal currents, waves, and wave-generated currents
is a complex process.
b. Tidal prism - channel area relationship.
(1) Initial research focused on the relationship to flow through the inlet and the minimum cross-sectional
area that could be sustained by that flow. O'Brien (1931, 1969) originally determined a relationship between
minimum throat cross-sectional area of an inlet below mean tide level and the tidal prism (i.e., the volume
of water entering or exiting the inlet on ebb and flood tide) at spring tide (Figure II-6-40). This relationship
was predominantly for Pacific coast inlets, where a mixed tidal pattern is observed and there typically is a
strong ebb flow between higher-high water and lower-low water. Jarrett (1976) continued the analysis and
performed regression analysis for various coastal areas with different tidal characteristics. A regression
equation is given for each of the Atlantic, Pacific, and Gulf coasts. Jarrett also recommended using O'Brien's
equation for dual-jettied inlets. The equations, in metric and English units, are given in Table II-6-3.
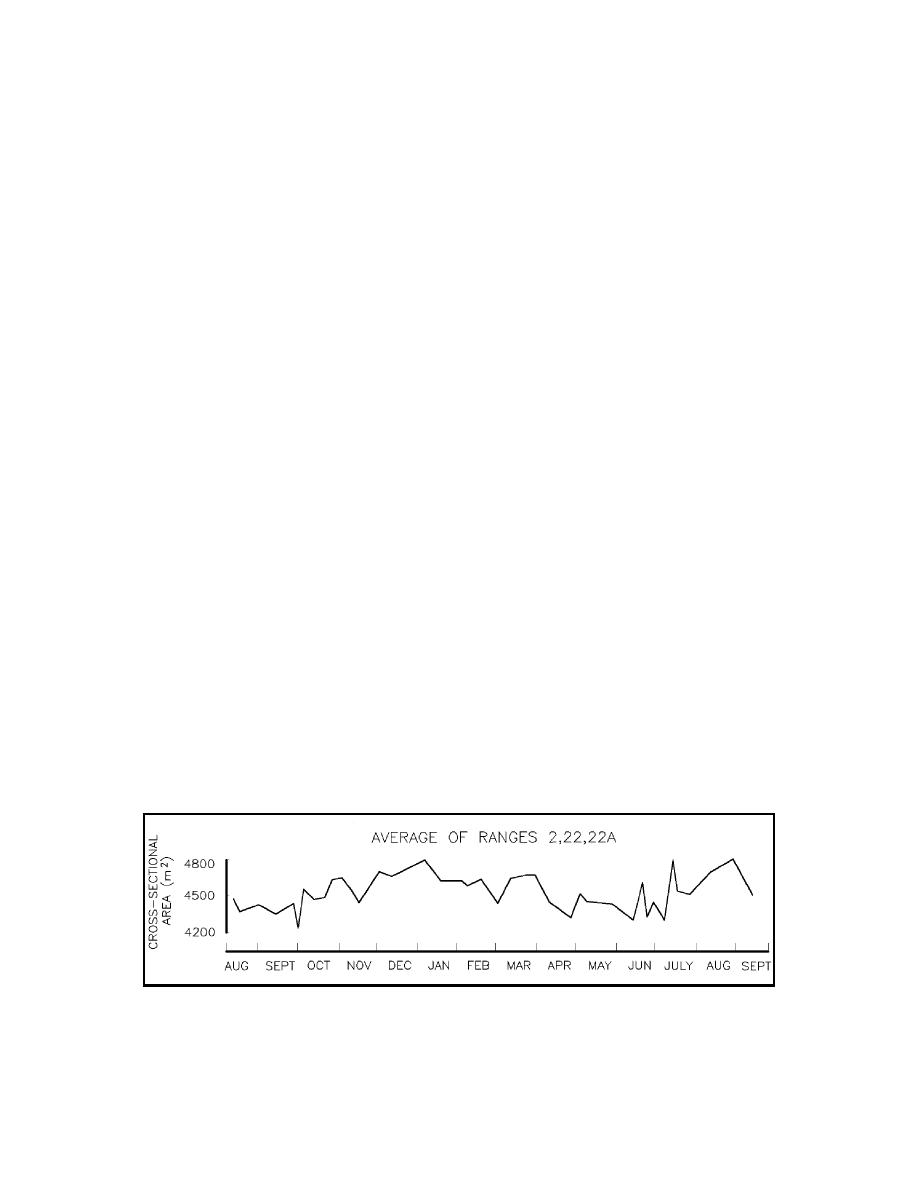
Figure II-6-40.
Variations in cross-sectional area for Wachapreaque Inlet (Byrne, De Alteris, and
Bullock 1974)
Hydrodynamics of Tidal Inlets
II-6-47



 Previous Page
Previous Page
