EM 1110-2-1100 (Part II)
30 Apr 02
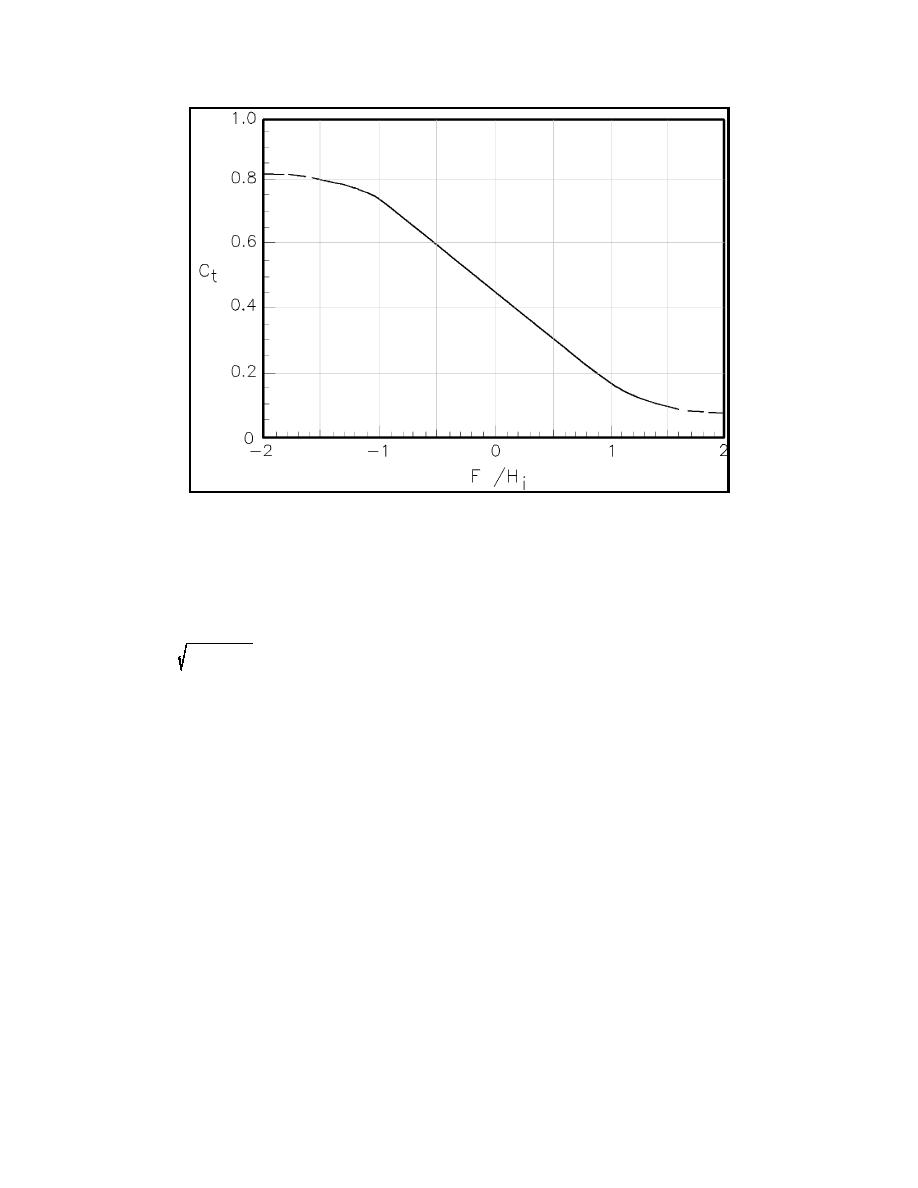
Figure II-7-19. Wave transmission for a low-crested breakwater (modified from Van
der Meer and Angremond (1992))
(b) When a porous rubble-mound structure suffers wave transmission caused by wave overtopping and
by wave propagation through the structure, the resulting combined transmission coefficient would be
2
2
Ct ' Ct t % Ct 0
(II-7-4)
where Ctt is the coefficient for wave transmission through the structure and Ct0 is the coefficient for wave
transmission by flow over the structure.
(c) Potential scale effects make it difficult to conduct scaled laboratory experiments to measure wave
transmission through rubble-mound structures. (Wave motion requires Froude similitude, while flow through
porous media requires Reynolds similitude, but the two are incompatible.) Consequently, the best procedure
for determining Ctt for a rubble-mound structure is a numerical procedure developed by Madsen and White
(1976). A computer program for applying this procedure has been developed by Seelig (1979,1980) and is
available in the ACES system (Leenknecht et al. 1992).
(d) The procedure developed by Madsen and White (1976) first calculates the amount of wave
dissipation caused by wave runup/rundown on the seaward face of the structure. (It is assumed that the wave
does not break - a good assumption for longer waves.) Wave reflection from the structure is also determined.
The remaining energy propagates into the structure and is partially dissipated by turbulent action. The
procedure then determines this rate of turbulent energy dissipation assuming a rectangular homogeneous
breakwater cross section that is hydraulically equivalent to the actual layered breakwater. This leads to the
transmitted wave height and Ctt. Application of this procedure requires a knowledge of the incident wave
height and period, the water depth, the breakwater layer geometry, and the stone sizes and porosities for each
layer. Seelig (1980) found that this procedure could be applied to irregular waves by using the mean wave
height and spectral peak period of the incident waves in the calculation.
II-7-22
Harbor Hydrodynamics



 Previous Page
Previous Page
